Разработка системы связи для передачи дискретных сообщений (способ передачи – амплитудная телеграфия), страница 4

В зависимости от того какая, гипотеза будет аксиомой, такой же будет плотность распределения (отличаются сдвигом на величину амплитуды сигнала(А))

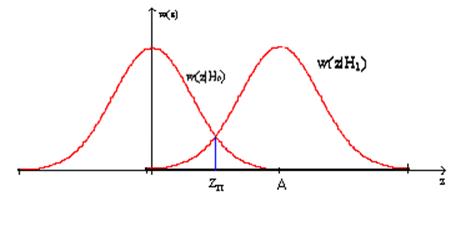
Рис № 6 График распределения плотности вероятности шумовой реализации при отсутствии сигнала, при наличии сигнала амплитудой A.

6. Случаи когерентного и некогерентного приёма Определение оптимального по критерию идеального наблюдателя порога, условные вероятности ошибок первого и второго рода, средняя вероятность ошибки, скорость передачи информации при наличии помех.

6.1. Когерентный прием.

Когерентный прием – прием сигнала, параметры которого полностью известны. Выясняем только наличие сигнала.

Плотности распределения вероятности (ПРВ):

Условная ПРВ для сигнал+шум W(z êН₁):

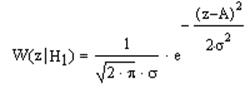
Условная ПРВ для шума W(z êН₀):

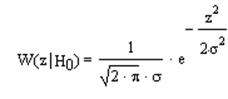
Вероятность ошибки первого рода (ложной тревоги) описывается следующим выражением:

,

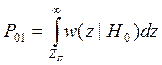где z_п – пороговый уровень.

В то же время вероятность ошибки второго рода (пропуск сигнала) описывается формулой:

.

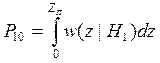Далее задача состоит в вычислении оптимального порога z_п.

 

Если значение будет лежать слева от z_п, то приемник будет считать, что передавался    символ 0, если справа, –  то 1.

Решением данного уравнения будет z_п, расположенный на пересечении графиков распределения p₀×w(z|H₀) и p₁×w(z|H₁).

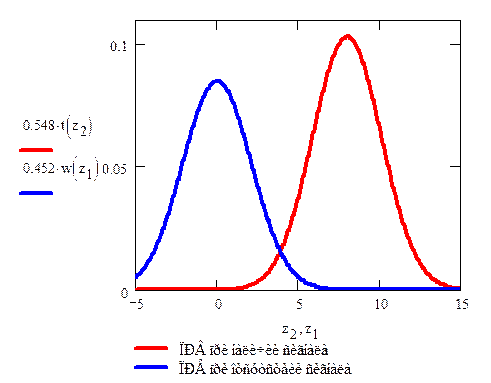
Рис. №7 Графики функций гауссовских плотностей вероятности для мгновенных значений сигнала  z.

Из графика определяем значение порогового значения z_п

                                                          z_п = 3,91  

В данной работе:

 w(z|H₀) = 1 / (2·3,14·4,5)^1/2·exp[-z²/4,5];

 w(z|H₁) = 1 / (2·3,14·4,5)^1/2·exp[-(z-8)²/4,5]

Подставляя z_п в выражения для ошибок 1 -го и 2 -го родов получаем:

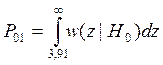
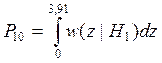
P₀₁ = 0,047

P₁₀ = 0,039

Средняя вероятность ошибки: Р_ош = Р₀× Р₀₁ + Р₁×Р₁₀

Р_ош = 0,452·0,067+0,548·0,027 = 0,021

Скорость передачи информации:

Взаимная информация:

,

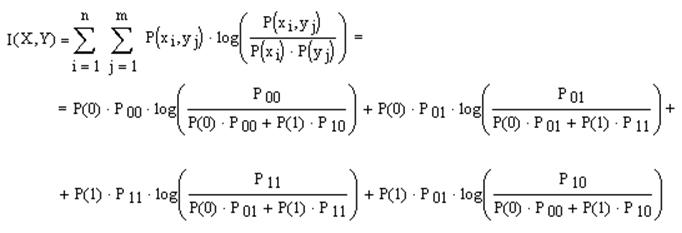где Р₀₀ и Р₁₁ найдем из соотношения:

,

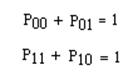тогда

           Р₀₀ = 1 – Р₀₁          Р₀₀ = 1 – 0,047 = 0,953

           Р₁₁ = 1 – Р₁₀          Р₁₁ = 1 – 0,039 = 0,961

Следовательно:

I(X,Y) = 0,452·0,953·1,076+ 0,452·0,047·(-3,543) + 0,548·0,961·0,811+0,548·0,047·   (-3,535)

I(X,Y) = 0,724 [бит]

I^/(X,Y) = 0,724/0,5·10^-6

 

Скорость передачи информации в канале с шумами:

I^/(X,Y) = 1,44·10⁶ [бит/c]

6.2. Некогерентный прием.

Некогерентный прием – прием сигнала, параметры которого известны не полностью.

Плотности распределения вероятности (ПРВ):

Условная ПРВ для сигнал+шум W(z êН₁):

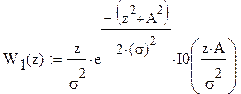
Условная ПРВ для шума W(z êН₀):

,

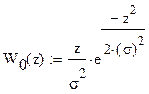тогда

            

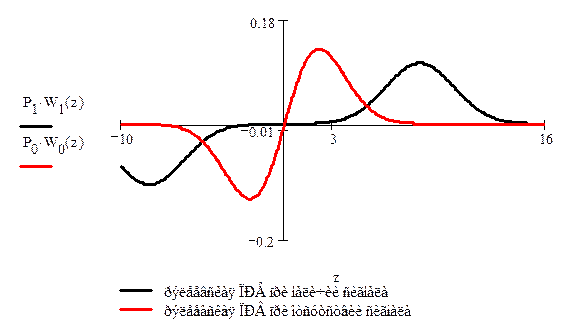
Рис. №8 Графики функций рэлеевских плотностей вероятности для мгновенных значений сигнала  z.

Из графика определяем оптимальный порог: z_п = 4,95.

Вероятность ошибки первого рода:

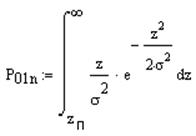
Вероятность ошибки второго рода:

,

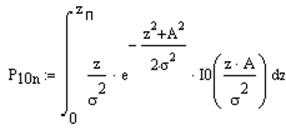тогда

P_01n = 0,066

P_10n = 0,054

Средняя вероятность ошибки:

Р_ош = Р(0)·Р_01n + Р(1)·Р_10n

Р_ош = 0,452·0,066+0,548·0,054

Р_ош =0,0595

Скорость передачи информации:

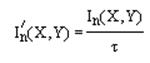
Взаимная информация:

,

где Р_00n и Р_11n найдем из соотношения:

Р_00n + Р_01n = 1

Р_11n + Р_10n = 1,

тогда

Р_00n = 1 – Р_01n                         Р_00n = 1 – 0,066 = 0,934

Р_11n = 1 – Р_10n                         Р_11n = 1 – 0,054 = 0,946,

следовательно

I_n(X,Y) = 0,452·0,934·1,048+ 0,452·0,066·(-3,054) + 0,548·0,946·0,787 +0,548·0,054·     (-3,085)

I_n(X,Y) = 0,668 [бит],

I^/_n(X,Y) = 0,668/0,5·10^-6

I^/_n(X,Y) = 1,34·10⁶[бит/с]

Сравнительный результат полученных данных.

Способ приема	Ошибка  первого рода  Р01	Ошибка  второго рода Р10	Средняя вероятность ошибки Рош	Скорость передачи информации
Когерентный	0,047	0,039	0,021	1,44 ·106
Некогерентный	0,066	0,054	0,0595	1,34·106

При когерентном способе перед приема мы выигрываем по всем параметрам вероятностям ошибок первого и второго рода, средней вероятности ошибки т.е. помехоустойчивость при когерентном приёме увеличивается.

7. Описание принципа корреляционной обработки и согласованной фильтрации; расчет фильтра.

7.1 Описание принципа корреляционной обработки и согласованной фильтрации

Для принятия пороговым устройством решения о пришедших из линии связи сигнале или паузе нужно вычислить корреляционный интеграл, а затем проверить неравенство: