Разработка системы связи для передачи дискретных сообщений (способ передачи – амплитудная телеграфия), страница 2

4.Рассчитать согласованный фильтр для приема элементарной посылки. Определить условные вероятности ошибок при приеме и среднюю вероятность ошибки. Оценить выигрыш в отношении сигнал/шум за счет согласованной фильтрации.

5.Составить обобщенную структурную схему системы связи для передачи дискретных сообщений, использующую помехоустойчивое (канальное) кодирование. Опираясь на результаты п.4, рассчитать вероятность двукратной ошибки в пределах одного кодового слова и охарактеризовать свойства кода по обнаружению и исправлению ошибок.

3.  Структурная схема системы связи, качественные временные диаграммы сигналов во всех промежуточных точках структурной схемы.  

И.с.b(t)Кодер     b_ц(t)  Модулятор              U(t)   Канал связи    ξ(t)   Помеха

z(t)

П. с.b(t)Декодер         b_ц(t)  Демодулятор

Рис.1 Обобщенная структурная схема системы связи для передачи дискретных сообщений

Сигнал b(t) поступает с выхода источника информации (И.с.) на вход кодера, где подвергается операции кодирования, необходимой для сокращения избыточности источника сообщения. Для передачи по каналу связи кодированный сигнал b_ц(t) отправляется на модулятор. Откуда поступает в канал связи, где модулированный сигнал U(t) подвергается воздействию на него помехи. В данном задании помеха аддитивная. z(t) является суммой принятого сигнала и помехи, причем помеха может быть не только канальная, но также может возникать из-за внутренних тепловых шумов в аппаратуре на приемной стороне. Назначение демодулятора состоит в выделении  огибающей ВЧ колебаний, пришедших с канала связи и, сравнивая уровень поступившего сигнала с пороговым значением, различает принятые сигналы, значит на декодер подаются кодовые комбинации. По ним декодер определяет исходный сигнал b(t), который получает приемник информации (П.с.)

В данной работе рассматривается способ передачи информации амплитудной телеграфией с пассивной паузой.  Это означает, что сообщение подвергается преобразованию в бинарный (двоичный) код. Для передачи «1» используется радиоимпульс, для передачи «0» -отсутствие радиоимпульса.

Временные диаграммы промежуточных сигналов

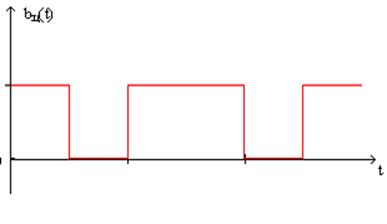
Рис.2 Сигнал на выходе кодера.

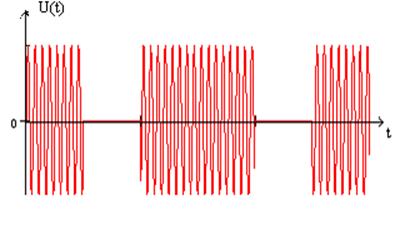
Рис.3 Сигнал на выходе модулятора.

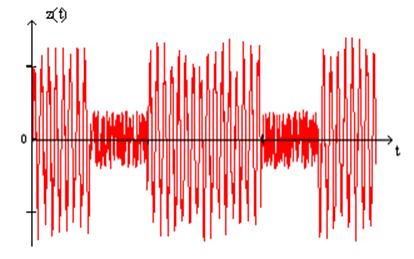
Рис.4 Сигнал + помехи на входе демодулятора.

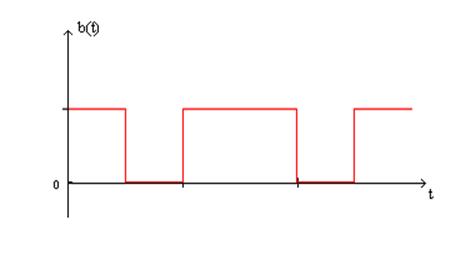
Рис.5 Восстановленный сигнал.

4. Определение энтропии, избыточности источника, кодирование, расчёт энтропии и избыточности кода, вероятности двоичных символов, передаваемых по каналу, скорости передачи информации по каналу без помех.

4.1. Кодирование символов с помощью кода Хаффмена.

На основе таблицы исходных данных кодируем алфавит с помощью кода Хаффмена, принимая символ с наименьшей вероятностью за ноль, а с большей за единицу, и кодируем символы в порядке увеличения их вероятностей.

Результат кодирования заносим в таблицу №2(см. следующую страницу):

Таблица №2 Кодовые комбинации соответствующие символам алфавита.

Закодируем фразу: Всембаденадеждапорока

Код фразы: 01011101001100011010011011100101011001101110000010110011010001110101001111001001

4.2. Определение энтропии, избыточности источника, скорости передачи информации.

Теорема Шеннона (в отсутствие шума): Среднее число кодовых символов, для передачи символов источника, с помощью кода с основанием m, можно как угодно приблизить к величине: Н(А) / log(m) , где m –число кодовых символов.