![]() <>
0.5×(Е1-Е2)
<>
0.5×(Е1-Е2)
В случае системы с пассивной паузой:
![]() <>
0.5×Е1
<>
0.5×Е1
В корреляционном приемнике такой интеграл формируется при помощи корреляторов и интеграторов. Коррелятор является нестационарным (параметрическим) устройством и включает в себя генератор опорного колебания, совпадающего по форме с ожидаемым сигналом, и интегратор, на выходе которого формируется значение, сравниваемое с порогом. Если в системе передачи информации используется много сигналов, то для каждого из этих сигналов нужно генерировать опорный сигнал с точностью до начальной фазы, на что нужно большое число корреляторов и интеграторов.
Поэтому возникает необходимость заменить корреляционную обработку фильтровой, т.е. вычислять корреляционный интеграл при помощи ЛИС-цепи.

Рис. № 9 принципиальная схема ЛИС – цепи
Физически – импульсная характеристика приближенно отображает реакцию цепи на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом цепи, например, периодом ее собственных колебаний.
Тогда сигнал y(t) на выходе ЛИС-цепи будет определяться интегралом Дюамеля:
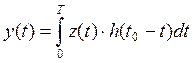 .
.
Считая сигнал полностью известным добиться корреляционного интеграла на выходе согласованного фильтра можно, положив равенство:
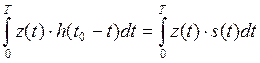 ,
,
откуда
![]() .
.
Соответственно АЧХ
согласованного фильтра в идеале должно иметь
такую же форму, как и модуль спектральной плотности сигнала ![]() .
.
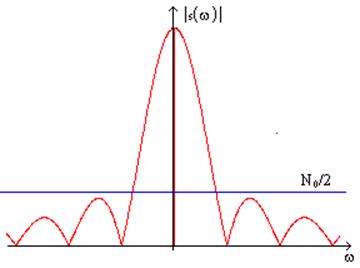
Рис. № 10. АЧХ согласованного фильтра.

Рис. №11. Структурная схема согласованного приемника.
При когерентном приеме амплитудный детектор не нужен, так как в любой момент времени фаза сигнала известна, и мы можем выбрать момент времени t0 такой, что сигнал окажется в своем максимуме.
В то же время при некогерентном приеме из-за помехи в сигнале на выходе детектора могут возникать неровности. В этих случаях применяется фильтр низких частот, имеющий функцию сглаживающего фильтра.
Завершающим шагом является обработка сигнала пороговым устройством , которое определяет передавался «0» или «1».
7.2.Расчет согласованного фильтра.
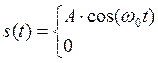 , на
интервале [0,t], t - длительность
одной посылки.
, на
интервале [0,t], t - длительность
одной посылки.
h(t) = s(t0
– t) = 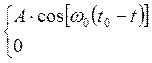
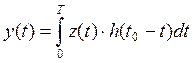 - сигнал на выходе
СФ, при z(t)
= s(t) + h( t) смесь сигнала с шумом
- сигнал на выходе
СФ, при z(t)
= s(t) + h( t) смесь сигнала с шумом
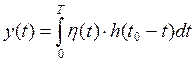 - сигнал на выходе
СФ, при отсутствии сигнала
(шумом).
- сигнал на выходе
СФ, при отсутствии сигнала
(шумом).
Плотность распределения вероятности для шума+сигнала:
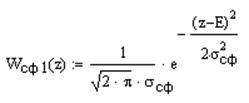
Плотность распределения вероятности для шума:
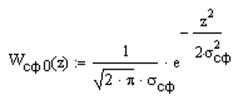 ,
,
где
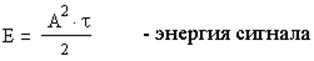
![]()
Вероятность ошибки первого рода:
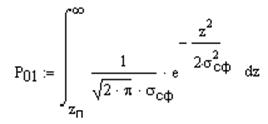
Вероятность ошибки второго рода:
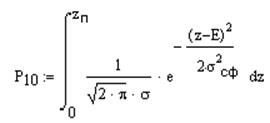 ,
,
где 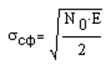 ,
, 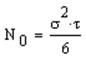

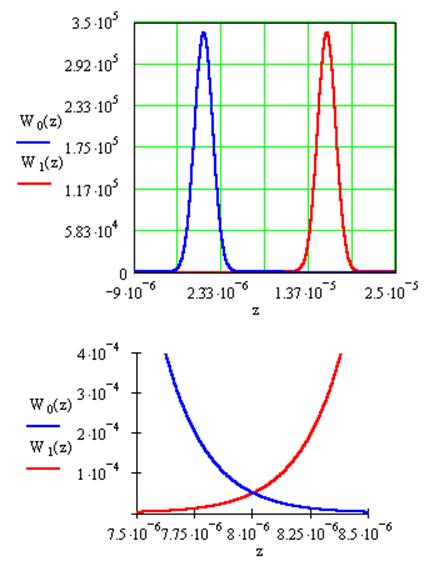
Рис. № 12 Графики ПРВ в присутствии и отсутствии сигнала в СФ.
zп = 8·10-6
Тогда вероятности ошибок:
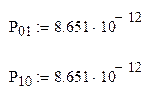
Средняя вероятность ошибки при когерентном приеме с использованием согласованного фильтра:
![]()
![]()
Отношение сигнал / шум на входе СФ(по напряжению):
qвх![]()
qвых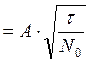 , где N0
=
, где N0
= 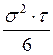
Q
= 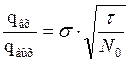
Q
= 1.18921·10-6·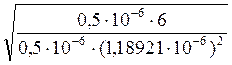
Q = 2,44
8. Помехоустойчивое кодирование, код Хемминга

Рис. № 13. Структурная схема системы связи для передачи дискретных сообщений при помехоустойчивом кодировании.
Кодирование источника кодом Хемминга является экономным кодированием и преследует цель повышения эффективности передачи информации, за счёт, замены исходного источника другим источником с меньшей избыточностью. Канале с помехами, то при приеме сигналов возникают ошибки, приводящие к искажению исходного сообщения. В таких случаях выдвигается на передний план задача повышения вероятности передачи правильных символов. Одним из путей ее решения является помехоустойчивое (канальное) кодирование.
Канальное кодирование применяют для большей помехоустойчивости. С этой целью в сигнал вводится некоторая избыточность, в данном случае это дополнительные, контрольные наборы символов. Если контрольные наборы символов, вычисленные приемником, не совпадают с контрольными наборами символов, принятыми им, то приемник фиксирует ошибку.
Принцип кода Хемминга состоит в том, что путем преобразования нескольких контрольных разрядов (наборов) удается не только обнаружить единичную ошибку, но и локализовать ее. Для двоичного кода определяется точное расположение неправильного разряда и его можно скорректировать путем инвертирования.
Используя k контрольных разрядов можно задать 2k различных комбинаций. При m информационных разрядах получается общая длина слова m + k. Дополнительные комбинации контрольных разрядов необходимы для определения, правилен ли полученный информационный код. Отсюда следует условие:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.