Если символы алфавита не равновероятны и независимы, то более вероятным символам ставятся в соответствие более короткие кодовые комбинации. Значит, для кодирования неоптимального источника нужно использовать неравномерный код. Для неравномерных кодов непременно должно выполняться префиксное условие: код должен быть неперекрываемым, т.е. никакая кодовая комбинация не является началом другой кодовой комбинации.
Производительность источника: Н'(А) = Н(А)/τ [Бит/с]
где τ-время выдачи одного символа
Скорость передачи информации:I’(А, В)xy = Ixy(А, В)/τ [Бит/с],
где Ixy(А, В) - количество информации, переданной от источника к приёмнику
Пропускная способность канала: С = max I’xy(А,В)
Теорема Шеннона (для канала с помехами): Если производительность источника меньше пропускной способности канала, то существует процедура кодирование-декодирование, при которой вероятность ошибочного декодирования сколь угодно мала.
А
) Если
Н'
С, то для
уменьшения вероятности появления ошибки кодовые комбинации нужно делать
большими, но это влечет за собой задержку во времени.
Б ) В противном случае ошибка неизбежна.
4.2.1. Расчёты энтропии, избыточности источника для источника.
Энтропия – это среднее количество информации, приходящееся на один символ.
Энтропия источника:
Hmax(А) – максимальная энтропия источника,
Н(А) max = -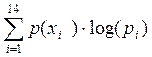
, но при
условии равных вероятностей, а это необходимо для достижения максимума, формула
сокращается до Hmax(А) = log214
Hmax(А) =3,808
Н(А) – энтропия источника,
Н(А) = -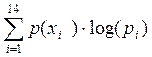 = -(0,121·(-3,047)+
0,113·(-3,146)+0,107·(-3,146)+0,099· (-3,336)+0,097·(-3,366)+0,089·(-3,49)+0,085·(-3,556)+0,083·(-3,591)+0,077·
(-3,699)+0,042·(-4,573)+0,041·(-4,608)+0,021·(-5,573)+0,014·(-6,158)+0,011·(-6,506))
Н(А) =3,209
c - избыточность источника,
c = (Hmax(А) – H(А)) / Hmax(А) = 0,157
4.2.2. Расчёты энтропии, избыточности кода, вероятности двоичных символов, передаваемых по каналу, скорость передачи информации по каналу без помех (СПИ)
μср - средняя длина кодовой комбинации,
μср=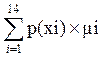
,
μср = 0,121·3+0,113·3+0,107·3+0,099·3+0,097·3+0,089·4+0,085·4+0,083·4+0,077·4+0,042· 5+0,041·5+0,021·5+0,014·6+0,011·6
μср = 3,617
Вероятность символа ноль: p(0)=
, где
νср=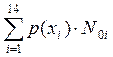
- среднее количество нулей,
Noi-количество нулей в i-ой кодовой строке,
P(xi)-вероятность символа xi, закодированного i-ой кодовой строкой
νср = 0,121·2+0,113·1+0,107·2+0,099·2+0,097·3+0,089·0+0,085·1+0,083·1+0,077·1+0,042· 2+0,041·3+0,021·3+0,014·2+0,011·3
νср = 1,634
p(0) = 1,634/3,617= 0,452
Вероятности p(0) и p(1) связаны соотношением: p(0)+ p(1)=1, откуда вероятность символа один:
p(1)=0,548
Энтропия для двоичного кода
Нк = -(0,452·log(0,452) + 0,548·log(0,548)) = 0,517992 + 0,475664 = 0,993656.
При передаче бинарного кода: Нк мах = μср bi=1 (исходя из условия равенства вероятностей сигналов)
Избыточность кода: χ к= (1-0,993656) / 1 = 0,006344288
Скорость передачи информации:I ' (А) = H (А) / τ· μср = 1,774398·106 бит/с.
5 Описание процесса принятия приемником решения при приеме сигнала.
На вход демодулятора поступает аддитивная смесь переданного сигнала и помехи, т.е. z(t)=S(t) + x(t)
В курсовой работе рассматривается канал с постоянными параметрами и аддитивной помехой, т.е. белый гауссовский шум.
Демодулятор в результате анализа принятой реализации смеси z(t) на интервале времени 0≤t≤τ устанавливает, какой из возможных сигналов S1(t) или S2(t) присутствует в наблюдаемом случайном процессе z(t), и принять решение о приеме символа 1 или 0. Для различения сигналов в приемнике необходимо устанавливать начало и конец интервала анализа каждой реализации z(t). Эта задача решается устройством синхронизации (позволяет определять начало и окончание каждого элемента сигнала). В данной работе предполагается, что синхронизация идеальна, т.е. моменты начала и окончания каждой посылки известны точно.
Гауссовский белый шум характеризуется нормальной плотностью распределения вероятности:
,
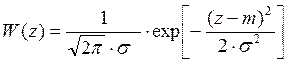где m – мат. ожидание, s2 – дисперсия шума.
Введем гипотезы: Н0 – «сигнала нет», Н1 – «сигнал есть»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.