MatLab в ТОС (Теория и обработка сигналов): Учебное пособие

help signal processing toolbox – выводит сведения  о функциях пакета Signal Processing Toolbox.

            Клавиши управления перемещением курсора «вверх» (key up) и «вниз» (key down) позволяют получить предыдущие команды командной строки в соответствующем порядке.

·  >> web http://www.mathworks.com  - загружает WEB- сайт фирмы Math Works Inc. - разработчика Matlab.

Векторы   и   матрицы

Самой характерной особенностью Matlab является то, что он является системой, предназначенной для вычислений с векторами, матрицами и полиномами.  Матрица – основной элемент Matlab. Вектор– это одномерный массив, матрица – двумерный. Вектор – это частный случай матрицы. Обычное число (скаляр) является матрицей размером (1 x 1), вектор – строка с  N элементами – это матрица размером  (1 x N),  вектор – столбец – матрица размером ( N х 1).

Векторы Matlab  могут определяться двумя способами.  Во-первых, вектор-строка  может генерироваться из элементов, заключенных в квадратные скобки и разделенных пробелами или запятыми.  Индексы  элемента массива всегда начинается с 1.

            Пример

» x=[5  2i  pi  7.1^2]

x =

  Columns 1 through 3

  5.0000e+000             0 +2.0000e+000i        3.1416e+000             

  Column 4

  5.0410e+001    

Доступ к элементам массива

» x(1)

ans =

     5        

Дополнение вектора элементом

» x(5)=12.7;

» x

x =

  Columns 1 through 3

  5.0000e+000                          0 +2.0000e+000i    3.1416e+000             

  Columns 4 through 5

  5.0410e+001                1.2700e+001     

Генерирование вектора – столбца

» x1 = [5; 7; 9]

x1 =

     5

     7

     9  

Транспонирование вектора

» x2=x1'

x2 =

     5     7     9

            Второй метод заключается в создании вектора с помощью выражения типа арифметической прогрессии.

Примеры

>> x =[0:0.2:1]                            %  Последовательность от 0 до 1 с приращением  0.2

        x =
  0  0.20     0.40      0.60      0.80        1.00

>>k = 0:10;             % Создается 1x11 вектор с элементами 0, 1, 2, ..., 10.

>> x1 = linspace(0, 4, 5)    % 1x5   вектор-строка – используется   команда    "linspace"

x1 =

     0     1     2     3     4

>> x = logspace (0, 1, 6)         %  6 значений от  10⁰ до 10¹  в логарифмической шкале

x =

     1.0000         1.5849             2.5119             3.9811 
      6.3096        10.0000

Ввод элементов матрицы выполняется в Matlab в квадратных скобках по строкам. Элементы строки матрицы разделяются пробелом или запятой, строки отделяются друг от друга символом  ‘;’ (точка с запятой).

Пример

» A= [1 2 3;  4 5 6;  7 8 9]     

A =

     1     2     3

     4     5     6

     7     8     9        

>> txt = 'string'                     %генерирование символьной матрицы/вектора

txt =

string

>> txt = ['s' 't' 'r'; 'i', 'n', 'g']  % ввод матрицы по отдельным символам

Специальные матрицы:

M = [];                               % пустая матрица

M = zeros(n,m);            % n x m матрица с нулевыми элементами

M = ones(n,m);              % n x m матрица из единичных элементов

M = eye(n);                      % единичная квадратная матрица n x n

M =   rand(m,n);                      % матрица размером m x n из случайных чисел,

                                                %  равномерно распределенных в интервале [0,1].

M =   randn(m,n);                    % матрица размером m x n из случайных чисел,

                                                %  распределенных по нормальному закону с нулевым

                                                %  средним значением и единичной дисперсией.

            Матрица может быть создана с помощью её блоков, например, если А – матрица размером 3 х 3, то команда

>> M = [A, zeros(3,2), ones(2,3), eye(2)];

создаст матрицу М размером  5 х 5.

Получение  элементов матриц

>>  x = A (1, 3)                        % формат доступа    A(<row>,<column>)

x  =

            3

>> y =A(2, :) 

y  =

4          5          6

» v1 = A(:, 2)

v1 =

     2

     5

     8
>> z = A(1:2, 1:3)

z  =

            1          2          3

            4          5          6

>>  v = A(:)                             %  преобразование матрицы в вектор

v =

            1

            2

            3

            4

            5

            6

Команда  length(x) возвращает размер (длину) вектора x,  команда size(x) –  размеры матрицы.

Пример

» length(A)

ans =

     3

Операции с матрицами

 MATLAB  имеет следующие операции с матрицами

+	сложение
-	вычитание
*	умножение
^	возведение в степень
'	транспонирование
/	правое деление
\	левое деление

Если размеры матриц несовместимы с матричной операцией, то выводится сообщение об ошибке.

Примеры

>> M1 = [1 7; -4 8];

>> M2 = [-1 0; 3 2];

>> H1 = [-2 5 -7; 3 1 2];

>> b2 = [9; 3];

>> A1 = M1 + M2                  %Сложение матриц

A1 =

     0     7

    -1    10

>> S2 = M2 - M1                    %Вычитание матриц

S2 =

    -2    -7

     7    -6

>> C1 = M1*H1                      %Умножение матриц

C1 =

    19    12     7

    32   -12    44

>> v1 = M1*b2                       %Умножение матрицы на вектор

v1 =

    30

   -12

            >> a = [1   2   3];         b = [4   5   6];

            >> v = a + b                            % сложение векторов

            v =   5              7              9

            >> d = a – b

            d =       -3         -3         -3

>> c = [9 3]                             %1x2 вектор-строка

c =

     9     3

>> c1 = c'                                % транспонирование вектора-строки

c1 =

     9

     3

Операции деления матриц требуют пояснения.

Если А – неособенная (обратимая) матрица, а b  - совместимый по размеру вектор,  то

>> y = A\b       %  Это  левое деление A на b , эквивалентно  решению системы  A * y = b

>> y = b/A      %   А это правое деление,  эквивалентно решению   y * A = b

Пример.

Пусть нужно решить систему уравнений

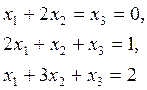
Решение системы в Matlab

» A=[1 2  1; 2  1  1; 1  3  1]

A =

     1     2     1

     2     1     1

     1     3     1

» b = [0;  1;  2]

b =

     0

     1

     2

» x = A \ b

x =

  3.0000e+000

  2.0000e+000

 -7.0000e+000

Поэлементные  операции  с массивами

В  Matlab имеются операции поэлементного преобразования массивов – векторов и матриц.

Такие операции называют операциями с точкой:

.*   -   поэлементное умножениемассивов,

 .^  -   поэлементноевозведение  в степень,

./   -    поэлементное деление,

 .\  -    поэлементное деление в обратном направлении.

Операции применяются к массивам одинакового типа и размера.

Примеры поэлементных операций с векторами 

» x=[1, 2, 3];     y=[4, 5, 6];

» z1 = x.*y

z1 =

     4    10    18

» z2 = y.^x

z2 =

     4    25   216

» z3 = y./x

z3 =

  4.0000e+000     2.5000e+000     2.0000e+000

» z4 = y.\x

z4 =

  2.5000e-001     4.0000e-001      5.0000e-001

Примеры поэлементных операций с матрицами 

>> A = [1  2; 3  4]

 A =

            1          2

            3          4

>> B =  A*A               %  Обычное умножение матриц

 B =

            7          10

            15        22

>>  C = A.*A              %  Поэлементное  умножение

 C =

            1          4

            9          16

» D = A./A                  %  Поэлементное деление

D =

     1     1

     1     1

Все элементарные функции Matlab являются функциями, аргументами которых могут быть  массивы.

Пример

» sin(A)

ans =

  8.4147e-001      9.0930e-001

  1.4112e-001      -7.5680e-001

Использование поэлементных  операций позволяет упрощать запись  математических выражений при вычислениях в Matlab

Пример.

Пусть требуется вычислить значения выражения       для  x  от 0 до  с шагом .  Вычисления в Matlab

» a = 2;   K = 5;

» x = 0 : pi/2/10 : pi/2;

» y = K * exp(-a*x).*sin(x)

y =

  Columns 1 through 6

            0  5.7130e-001    8.2428e-001    8.8451e-001    8.3645e-001    7.3497e-001

  Columns 7 through 11

            6.1419e-001       4.9407e-001     3.8519e-001    2.9218e-001    2.1607e-001

ПрограммированиевMATLAB

Выше рассматривались примеры вычисление в Matlab в режиме калькулятора. Несмотря на значительные возможности и широкое использование на практике этот режим имеет существенные недостатки. В нем нельзя повторить вычисления без повторного набора всех команд, невозможно возвратиться назад и т.д. Работа в этом режиме не является программированием. Поэтому сколько – нибудь сложные вычисления требуют, как правило, программирования на языке Matlab  и записи программ  в виде М – файлов