Лекція №3. Масштаби карт і планів.
План лекції:
1. Поняття про чисельний, лінійний і нормальний поперечний масштаби. Точність масштабу.
Горизонтальні проекції ліній місцевості не можуть бути відкладені на папір в натуральну величину. Щоб відкласти довжину лінії на папері, її необхідно зменшити. Ступінь зменшення ліній при відкладанні їх на папері називається масштабом карти (плану): 1/m=d/D (1)
В багатьох випадках горизонтальна проекція мало відрізняється від довжини самої лінії, тому іншими словами - масштабом називається відношення довжини .лінії на карті до довжини відповідної лінії на місцевості. Це відношення можна написати у вигляді дробу, чисельник якого дорівнює одиниці, а знаменник числу, яке показує в скільки разів зменшені зображені лінії на карті. Наприклад: 1:25000, 1:10000, 1:5000. Масштаб, виражений відношенням чисел називається чисельним (числовим). Зображення на кари більше, якщо знаменник масштабу менший і навпаки. За допомогою чисельного масштабу па практиці розв'язують дві наступні задачі:
1. Знаючи довжину лінії на місцевості, вирахувати ту довжину, яку вона повинна мати в даному масштабі на плані.
2. Знаючи довжину лінії на плані, вирахувати її довжину на місцевості.
Перша задача розв'язується діленням довжини лінії на зменшений в 100 раз знаменник чисельного масштабу: d = Д100/м (2)
Друга задача є оберненою першій і розв'язується множенням довжини лінії на плані на зменшений в 100 раз знаменник чисельного масштабу.
Наприклад: Д = dм/100 (3)
1. Визначити довжину лінії на плані dПЛ, якщо відома довжина цієї лінії на місцевості dm=130.7 м, масштаб плану 1:1000, dПЛ = dm:n; n - число метрів на місцевості, яке відповідає 1 см на плані в заданому масштабі n=1000:100=10 м dПЛ=130.7:10= 13.1 см
2. Визначити довжину лінії на місцевості, якщо довжина її на карті dПЛ=5.3см, а масштаб карти 1:10000, n=10000:100=100 м. dm=5.3100=530 м.
На практиці для розв'язання двох попередніх задач не вдаються до множення та ділення, а користуються спеціальною графічною побудовою, яка називається лінійним масштабом.
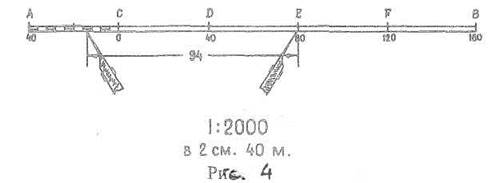
Для побудови лінійного масштабу беруть пряму лінію АВ і на ній декілька раз відкладають який-небудь відрізок АС, переважно 2 см (Рис.4). Цей відрізок називається основою масштабу. Перший з лівої сторони відрізок АС поділяють на десять рівних частин, для того, щоб можна було вимірювати на карті і відкладати на ній десяті частини основи масштабу. За початок відліку довжин беруть штрих між першим і другим великим відрізками (основами) лінійного масштабу і відмічається "о" вправо від нуля підписують числа, які відповідають цілим основам масштабу, а зліва від нуля - його частини, така десята частина називається найменшою поділкою масштабу. За допомогою такого масштабу сотні і десятки метрів відраховуються безпосередньо, а окремі метри оцінюються приблизно. Всяка лінійка з сантиметровими і міліметровими поділками може бути використана як графічний масштаб, Якщо потрібно виміряти на карті віддаль між точками А і В, то для цього голки вимірника прикладають до точок А і В карти, а потім прикладають вимірник до лінійного масштабу так, щоб ліва ніжка припадала зліва від нуля, а права попадала точно на яку-небудь поділку вправо від нуля. Віддаль між точками А і В буде дорівнювати сумі відліків по двох ніжках вимірника, частини малих поділок визначаються приблизно.
Щоб підвищити точність вимірювання і відкладання ліній на плані (карті), використовують так званий поперечний масштаб. Поперечний масштаб будують в такий спосіб:
на прямій лінії КL декілька раз відкладають основу масштабу. Основу масштабу, як правило беруть 2 см (Рис. 5).
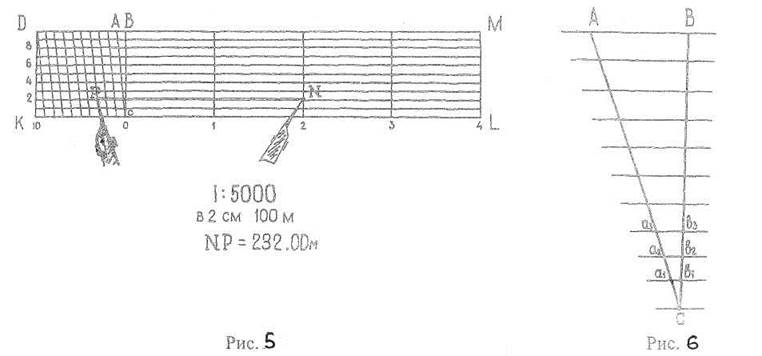
Із всіх одержаних таким способом точок проводять перпендикуляри. Два крайні перпендикуляри КD і LМ поділяють на десять рівних частин і через ці мітки проводять прямі паралельно до лінії КL. Перший лівий відрізок КС і DВ також поділяють на десять рівних частин і ці мітки з'єднують між собою скісними лініями в такій послідовності:
Початок верхньої лінії з кінцем першої поділки нижньої лінії, кінець першої поділки верхньої лінії - з кінцем другої поділки нижньої лінії і т.д. Розглянемо трикутник АВС (Рис. 13). Із подібності трикутників АВС і a1Cb1 запишемо: a1b1/AB=Cb1/CB; a1b1=Cb1AB/CB.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.