Рівнокутна поперечно-циліндрична проекція Гауса

Лекція №12. Рівнокутна поперечно-циліндрична проекція Гауса

План лекції:

1.  Загальні поняття про рівнокутну, поперечно-циліндричну проекцію Гауса.

2.  Формули обчислення координат Гауса за геодезичними координатами.

3.  Формули для обчислення геодезичних координат за координатами Гауса.

1. Загальні поняття про рівнокутну, поперечно-циліндричну проекцію Гауса

Для геодезичних цілей необхідно, щоб проекція була рівнокутної, а перекручування довжин ліній і площ були б незначними й виправлення внаслідок цих перекручувань обчислювалися б по простих формулах. У загальному випадку при зображенні еліпсоїда на площині можна обчислити всі виникаючі перекручування, як би великі вони не були. Але тоді губиться зміст переходу на площину, тому що обчислення більших перекручувань (виправлень) у багатьох випадках представляє не менш складне завдання, чим обробка геодезичних вимірів безпосередньо на еліпсоїді. Тому для геодезичних цілей на площині зображують невелику область поверхні еліпсоїда, у межах якої перекручування ще невеликі й обчислюються порівняно просто. Якщо ж потрібно зобразити більшу область, її ділять на окремі малі ділянки (зони), і кожна ділянка зображується на площини у своїй системі плоских координат.

Найбільш широко в практиці геодезичних робіт застосовується поперечно-циліндрична проекція Гауса. Рішення про введення в СРСР однакової системи прямокутних координат Гауса в шестиградусних зонах було прийнято в березні 1928 р. на Третій геодезичній нараді по доповідях професорів В. В. Коврайського, Н. Н. Матусевича і Н. Г. Келля.

Поперечно-циліндрична рівнокутна проекція еліпсоїда була розроблена в 1825-1830 р. німецьким геодезистом і математиком Гаусом. В 1912 р. німецький геодезист Крюгер одержав робочі формули прямокутних координат як функції геодезичних. Саме тому проекцію стали називати проекцією Гауса-Крюгера. Однак згодом відомі вчені запропонували багато інших більше зручних формул цієї проекції, що дає підставу називати проекцію тільки по імені її автора - Гауса.

Проекція Гауса — це рівнокутна проекція еліпсоїда з постійним масштабом вздовж середнього меридіана. При стиску, рівному нулю, тобто в окремому випадку, це поперечна меркаторська проекція кулі. Тому в деяких країнах, наприклад у США, Англії, проекцію Гауса називають поперечною проекцією Меркатора й застосовують її в трьох- і шестиградусних зонах.

При використанні проекції Гауса земний еліпсоїд розділяється на зони меридіанами. Кожна зона являє собою сфероидический двуугольник, обмежений меридіанами й побудований від одного полюса до іншого. Середній меридіан у кожній зоні називається осьовим, і його довгота позначається буквою L₀.

У кожній зоні зображення осьового меридіана приймається за вісь абсцис, а зображення екватора - за вісь ординат. Ці криві еліпсоїда (осьовий меридіан і екватор) зображуються на площині прямими лініями. Отже, у кожній зоні є своя система й свій початок координат у перетинанні осьового меридіана й екватора.

У проекції Гауса поверхня шести- або триградусної зони зображується з помітними перекручуваннями, але достоїнством її є порівняльна простота й висока точність обліку цих перекручувань. 

Розглянемо завдання, які виникають при проектуванні поверхні еліпсоїда на площину.

Нехай на еліпсоїді (мал. 36) побудований сфероидический трикутник CDE, у якому обмірювані всі кути, сторона CD і її геодезичний азимут А. Відомі координати В, L крапки С. Побудуємо дугу малого кола (паралель) СТ, паралельну осьовому меридіану. Тоді кут у буде виражати геодезичне зближення меридіанів.

На площині осьовий меридіан ОР проектованої зони й екватор  0Q зображуються взаємно перпендикулярними лініями, твірної лінії абсцис ох і ординат оу системи координат Гауса.

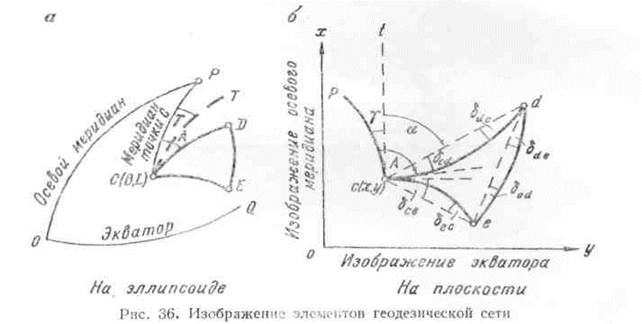
Меридіан СР точки С зобразиться на площині кривій СР, а паралель СТ — лінією, паралельної осьовому меридіану так, що кут = PCt зобразиться без перекручувань, тобто рівним куту РСТ внаслідок властивості рівнокутності проекції.

Трикутник CDE зобразиться криволінійними сторонами, не даними відповідним сторонам на еліпсоїді, але утворюючі кути, рівні проектованим.