Для забезпечення рішення плоских трикутників криволінійні сторони заміняють їхніми хордами, а кути виправляють відповідними виправленнями в напрямки. Малий кут 8cdміж кривою, що зображує дану сторону на площині, і її хордою називається виправленням напрямку за кривизну зображення геодезичної лінії на площині.
Сторони трикутника - лінійні елементи геодезичної мережі - зображуються в проекції Гауса з перекручуваннями відповідно до зміни приватного масштабу. Тому при проектуванні довжин ліній з еліпсоїда на площину в проекції Гауса в них уводяться відповідні виправлення, називані редукціями відстаней.
Орієнтування лінії СD на еліпсоїді пов'язане з напрямком на північ геодезичного меридіана
даної крапки С и визначається азимутом А лінії CD. На площині кутом, що
орієнтує, є дирекційний кут α лінії cd, вимірюваний щодо позитивного напрямку осі абсцис або
лінії, паралельній осі абсцис, і відлічуваний по ходу годинниковий стрілки від 0°до 3600 . Дирекційний кут хорди cd
відрізняється від геодезичного (істинного) азимута на величину зближення
меридіанів 
і величину виправлення напрямку за
кривизну зображення геодезичної лінії на площині δСD
А = а + γ + 8cd
Таким чином, при проектуванні (переносі) геодезичної мережі з поверхні еліпсоїда на площину й назад виникають наступні завдання:
а) обчислення прямокутних координат Гауса х, у на площині, як функції геодезичних координат В, L;
б) обчислення геодезичних координат В, L по прямокутних координатах х, y;
в) визначення характеру зміни масштабу зображення;
г) обчислення зближення меридіанів γ;
д)обчислення виправлень за кривизну геодезичної лінії на площині для кожного обмірюваного в тріангуляції напрямку;
е) обчислення редукції довжини вихідної сторони за перехід з еліпсоїда на площину;
ж) переобчислення прямокутних координат з однієї зони в іншу.
2. Формули обчислення координат Гауса за геодезичними координатами.
Координати точок у проекції Гауса коротко називають координатами Гауса.
За умовами проекції абсциси х крапок у координатах Гауса рівні сфероидическим абсцисам хс, тому,
х=Х+Nt”2/2ρ”2 sinBcosB + Nt”4/24ρ”4sinBcos3B(5 — tg2B). (1)
Але ординати yточок у координатах Гауса не рівні їх сфероидическим ординатам ус. Ординати точок у треба одержувати з умовою масштабу
n=1+y2c/2R2.
Таким чином формулою користуватися не можна. Не приводячи висновків, напишемо, що ординати точок yодержують по формулі
y=l”/ρ”NcosB+t”3/6ρ”3Ncos3B(1-tg2B). (2)
Нагадаємо, що по формулах (1) і (2) можна робити обчислення в межах двоградусної зони, тобто при l <=10. При l > 1° застосовують повні, значно більше складні формули .
Обчислення по цих повних формулах досить громіздкі, складні й трудомісткі. Тому на підставі їх для полегшення
обчислень складені спеціальні «Таблиці для обчислення плоских координат Гауса». Для зручності користування таблицями й скорочення записів при обчисленні ці формули при складанні таблиць перетворені й наведені до виду рядів по ступенях l і y. Не розкриваючи виражень окремих членів цих рядів, приведемо в остаточному виді практично застосовувані формули:
х - X = агl2+ а4l4 + а’k6; х = Х + ( х-Х),
y = b1
l
+ b3l3 + b’k5 ; = c1l + c3l3
+ c'k5. (3)
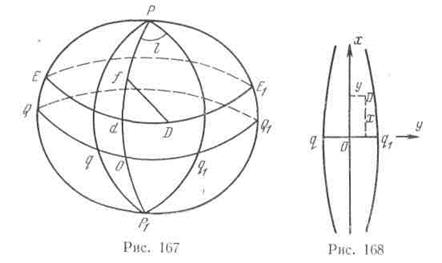
На мал. 167 показано визначення точки на поверхні еліпсоїда прямокутними сфероидическими координатами й на мал. 168 визначення цієї ж точки координатами Гауса. Для виключення негативних значень ординат ординати крапок на осьовому меридіані приймають рівними 500 км. Такі координати називають «перетвореними».
3. Формули для обчислення геодезичних координат за координатами Гауса
Формули для обчислення геодезичних координат по плоских координатах Гауса
B=B1 – (dB/dg) (g1 – g) – (d2B/dg2)1 (g1 – g)2/2 - …=
=
B1 – ρ”y2V21t1/2N21
+ ρ”y4t31/8N41 (1 + 4
2 + 34)
+ …,
l = y (dg/dX)1 – y3/6 (d3g/dX3)1 + … =
=
ρ”y/N1cosB1 – ρ”y3/6N31cosB1
(1 + 2t21 + 21)
+ ….
Нагадаємо, що довготу меридіана обумовленої крапки одержують по формулі
L=L0 + l
При обчисленні геодезичних координат по прямокутним використовують спеціальні таблиці.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.