Прив'язка зйомочних ходів засічками. Обернена засічка (задача Потенота)

Лекція 23. Прив'язка зйомочних ходів засічками.

       План лекції:

1.  Пряма, кутова та лінійна засічки.

2.  Обернена засічка (задача Потенота).

1.  Пряма, кутова та лінійна засічки

Спосіб прямої засічки

Прямою засічкою положення точки с, яка відповідає точці С місцевості, визначають за позначеними на планшеті точками А і В (рис.1). У точці А планшет орієнтують за напрямом ab. Після цього скошене ребро лінійки кіпрегеля прикладають до точки а, зорову трубу наводять на віху, встановленому в точці С і прокреслюють напрям am. Потім переходять з мензулою в точку В і орієнтують планшет за напрямом ba. Приклавши лінійку кіпрегеля до точки b, зорову трубу наводять на точку С і прокреслюють лінію bn. Точка с перетину ліній am s bn відповідає точці С місцевості.

Рис. 1. Пряма графічна засічка

Визначення координат планових розпознаків прямою засічкою застосовують у відкритій місцевості і в тих випадках коли на розпознаку неможливо установити інструмент. Пряма засічка виконується не менше ніж з трьох вихідних пунктів.

При визначенні координат розпознака прямою засічкою (Рис. 2) в трикутниках 12Р і 23Р теодолітом на пунктах тріангуляції, координати яких відомі (Х₁, У₁ Х₂ У₂ і X₃ У₃) міряють кути β₁, β₂, β₃, β₄.

Використовуючи виміряні кути і координати пунктів тріангуляції, користуючись формулами котангенсів кутів трикутника (формули Юнга), двічі обчислюють координати розпознака.

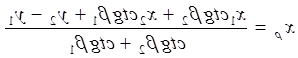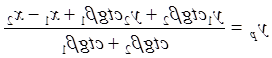Розходження координат не повинно перевищувати подвійної граничної точності масштабу

створюваної карти. При користуванні формулами Юнга нумерація кутів і пунктів тріангуляції виконується за правилом: якщо стати на сторону між вихідними пунктами тріангуляції (1,2) обличчям до розпознака, то пункт і кут з лівої сторони будуть "1", а з правої сторони "2".

В випадках, коли між суміжними пунктами тріангуляції 1, 2 і 2, 3 немає видимості, але є видимість на інші суміжні пункти (4,5,6,7.8) (Рис. 3), то для обчислення координат розпознака користуються формулами тангенсів або котангенсів дирекційних кутів (формули Гаусса). З цією метою на пунктах тріангуляції 1,2.3 теодолітом міряють прилеглі кути β₁, β₂, γ₁, γ₂, δ₁, δ₂.. Маючи дирекційні кути ліній 1-4, 1-5, 2-6, 2-7. 3-4, 3-8, які уміщуються в каталогах координат пунктів тріангуляції або обчислюються за. координатами пунктів, розв'язуючи обернені геодезичні задачі і виміряні прилеглі кути обчислюють дирекційні кути напрямів α_1-р; α_2-р; α_3-р з пунктів тріангуляції на розпознак. Користуючись формулами Гаусса двічі обчислюють координати розпознака.

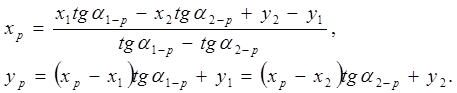Рис. 3

Якщо один з дирекційних кутів (α_1-р; α_2-р; α_3-р) близький до 90°або 270° (в межах ±15°), то для обчислення координат розпознака застосовують формули котангенсів дирекційних кутів.

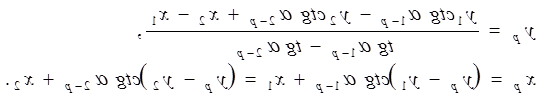Координати розпознака обчислюють спочатку з однієї пари, а потім з другої пари напрямків.

При допустимій різниці координат планових розпознаків, одержаних з двох обчислень, обчислюють середнє значення координат розпознака.

Лінійна засічка

З застосуванням в геодезичній практиці різних фазових віддалемірів, стало можливим визначати координати розпознаків лінійними засічками. З цією метою міряють віддалі між розпознаком "Р" і пунктами тріангуляції "А" і "В" (Рис. 4).

Рис. 4

По виміряних лініях "а" і "b" і координатах пунктів тріангуляції А і В обчислюють координати розпознака. За допомогою координат пунктів тріангуляції "А" і "В" обчислюють дирекцїйний кут лінії α_AB і її довжину АВ=Р. Таким чином в трикутнику АРВ відомі всі три сторони a, b, p, можна обчислити всі три кути користуючись формулою:

a²=b² + p² - 2bpcosA      

Якщо кути обчислені правильно, то сума всіх трьох кутів трикутника повинна дорівнювати 180⁰.

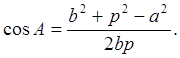Обчисливши всі кути трикутника А

    α_АР = α_АВ - кутА                               α_ВР=α_АВ±180⁰+кутВ       і маючи виміряні сторони АР=b і АР=а, двічі обчислюють координати розпознака