Δх1=bcosαAP Δy1=bsinαAP
Δx2=acosαBP Δy2=asinαBP
Xp=xA+Δx1 yp=yA+Δy1
Xp=xB+Δx2 yp=yB+Δy2
Якщо розходження обчислених координат розпознака не перевищує допустимої величини, то обчислюють середнє з двох обчислених значень.
2. Обернена засічка (задача Потенота)
Сутність оберненої багаторазової засічки полягає у визначенні положення четвертої точки, наприклад М, відносно трьох даних точок А, В і С, які не знаходяться на одній прямій. Якщо відомі два кути β і γ (Рис. 5,а), вершиною яких є точка М3, а сторонами - напрями М3А, М3В і М3С, не установлюючи мензулу в точках А, В і С. Шукана точка М відносно трьох відомих А, В і С може займати одне із шести положень:
М1 - точка знаходиться в середині трикутника АВС;
М2 - на одній із сторін трикутника АВС;
М3 - між одною із сторін трикутника АВС і колом, проведеним через три точки А, В і С;
М4 - на колі, яке проходить через точки А, В і С;
М5 - за колом проведеним через три точки А, В і С;
М6 - за колом, але в середині кута, утвореного продовженням двох будь-яких сторін
трикутника АВС.
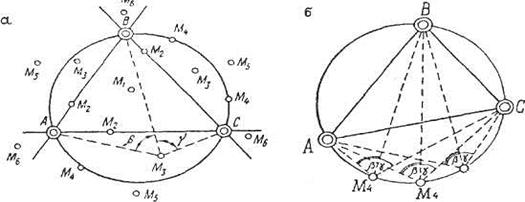
Якщо точка М знаходиться на одній із сторін трикутника АВС, то її положення на планшеті визначають способом комбінованої засічки.
Якщо точка М попадає на коло, то для її визначання недостатньо знати тільки кути β і γ, тому що на колі можна мати безліч точок і кожна з точками А, В і С будуть пов'язані одними і тими кутами β і γ (Рис. 5,б). В цьому єдиному випадку розв'язання задачі є невизначеним, тому для розв'язання оберненої засічки необхідно мати на місцевості і на планшеті чотири точки і двічі розв'язати задачу, виключаючи кожний раз одну з відомих точок.
Ця задача є більш точним, але й більш складним варіантом зворотної засічки. ЇЇ перевагою є те, що для вирішення задачі потрібна лише одна постановка мензули в точці, положення якої на плані (планшеті) визначається.
Для визначення положення точки М (рис.6, а) за даними пунктами А,ВіСу точці М треба виміряти кути α і β. Якщо координати вказаних пунктів відомі, то задачу по обчисленню координат точки М можна вирішити аналітичним шляхом. Існує багато способів вирішення цієї задачі.
Якщо пункти А, В і С нанесені на мензульний планшет за координатами або одержані при побудові геометричної сітки, то цю ж задачу можна вирішити графічним способом.
Теорія графічного вирішення цієї задачі полягає в наступному. Нехай на планшет нанесено точки А, В і С. Припустимо, що положення точки т, яка відповідає точці М місцевості, знайдено (рис. 6, б). Проведемо через точки С, т і В коло, продовжимо лінію Ат до перетину з цим колом і одержимо допоміжну точку Z. З'єднаємо точки С і В між собою і з точкою Z прямими: пініями. Кути 180°-а і 1800-β при точці т відповідно дорівнюють кутам при точках В і С як кути, що спираються на одні й ті ж дуги. Отже, кут між стороною ВС і продовженням сторони ZB дорівнює куту α, а кут між стороною СВ і продовженням сторони ZС - куту β. Відзначимо також, що кути φ і γ при точці Z дорівнюють таким же кутам відповідно при точках В і С.
На цій підставі положення точки т на планшеті можна знайти за виміряними на місцевості кутами а і β наступним чином. Виміряний при точці М лівий кут а (рис. 6, а), будують на плані транспортиром при правій точці В від лінії ВС (рис. 6, в). Кут β відкладають транспортиром при лівій точці С від лінії СВ. На перетині двох ліній, проведених з точок В і С, одержимо допоміжну точку Z. Шукана точка т лежить на прямій AZ. Отже, якщо поставити мензулу в точці М місцевості, прикласти ребро лінійки кіпрегеля до точок А і Z на планшеті і, повернувши планшет, навести на точку А місцевості, то він буде орієнтований. Тому лінію АZ називають лінією орієнтування. На перетині кола, проведеного через точки С, В і Z, з лінією орієнтування одержимо точку т.
На практиці для графічного вирішення задачі Потенота користуються способами Бесселя, проф. Болотова, послідовних наближень та іншими.
|
|
Рис. 6. Графічне вирішення задачі Потенота
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.