Поняття про корелатний спосіб зрівнювання. Спрощене зрівнювання центральної системи

Лекція № 19. Кінцеве обчислення. Задача зрівнювання.

         План лекції:

1.  Поняття про корелатний спосіб зрівнювання.

2.  Спрощене зрівнювання центральної системи.

1.  Поняття про корелатний спосіб зрівнювання

Загальні положення з вирівнювання геодезичних мереж корелатним способом

Нині існує багато методів вирівнювання геодезичних мереж. Найбільш поширеним є вирівнювання мереж корелатним або параметричним методом.

Розглянемо суть вирівнювання геодезичних вимірів корелатним методом. Нехай у геодезичній мережі виконано n вимірів, які приводять до виникнення r умов (при цьому r<n). Припустимо, що найімовірніші значення виміряних величин M₁, M₂ ..., M_n будутьM₁, M₂ ..., M_n.Нехай у даній мережі можна скласти r рівнянь, які мають вигляд:

(1)

Якщо у рівняння (1) замість найімовірніших значень виміряних величин підставити їх виміряні значення, отримаємо:

(2)
       де W₁, W₂, ..., W_r - вільні члени (нев'язки).

Уявимо, що кожне найімовірніше значення виміряної величини можна виразити:

        (3)

Тоді система рівнянь матиме вигляд:

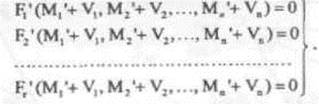     (4)

Розглядаючи кожне із рівнянь системи (4) у ряд Тейлора, маємо:

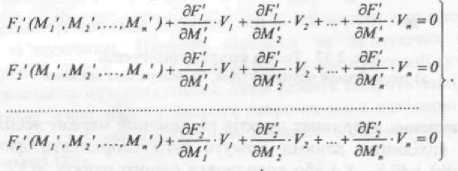   (5)

Уведемо позначення для першого рівняння

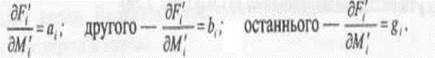
Із врахуванням наших позначень система рівнянь (5) набуде вигляду:

Розв'язок задачі вирівнювання полягає у знаходженні поправок V₁, V₂, ..., V_n до виміряних значень величин М₁', M₂', ..., M_n'. Однак труднощі у вирішенні цієї задачі полягають у тому, що кількість невідомих n більша від кількості рівнянь r (n>r). Розв'язок системи (6) виконують, використовуючи невизначені множники Лагранжа (корелати) k_i. З цією метою складають нормальні рівняння (7), які мають вигляд:

Із розв'язку рівнянь системи (7) знаходимо корелати k_i, а потім за відомими формулами поправки у виміряні кути(8):

Вирівнювання тріангуляції корелатним методом

Нагадаємо, що тріангуляція – це метод побудови геодезичної мережі за допомогою трикутників, в яких виміряні тільки кути. Поряд їз цим для побудови мережі використовують такі фігури, як геодезичний чотирикутник та центральну систему (рис.1).

Рис. 1 Типові фігури в тріангуляції:

а) геодезхичний чотирикутник, б) центральна система

Для обчислення координат пунктів геодезичної мережі необхідні вихідні дані. Такими вихідними даними можуть бути координати двох суміжних пунктів А(Х_А, У_А) і В(Х_В, У_В) або координати одного пункту А(Х_А, У_А), вихідна сторона S_А-В та вихідний дирекційний кут α_АВ (рис. 2).

Рис. 2 Вихідні дані для обчислення координат пунктів:

а) координат двох вихідних пунктів; б) координати одного вихідного пункту, вихідна сторона та вихідний дирекційний пункт

Мережу тріангуляції, у якій є тільки необхідні вихідні, називають вільною. Якщо в мережі є надлишок вихідних даних, то вона є невільною. Наприклад, мережа тріангуляції (рис.3) є невільною, оскільки в ній, крім вихідних координат пунктів А і В, є додаткові координати пункту F(X_F, Y_F).

Рис. 3 Невільна мережа тріангуляції

Зауважимо, що під час вирівнювання тріангуляції виникає завдання обчислення сторін трикутників мережі. Для цього використовують теорему синусів. Наприклад, для отримання значення сторони ВС, коли відома сторона S_А-В та кути у трикутнику АВС (рис.3), вона має вигляд:

У мережі тріангуляції сторони, які є спільними для двох трикутників, називають зв'язуючими. Напроти вихідних та зв'язуючих сторін лежать зв'язуючи кути (1, 3, 4, 6, ..., 12). При цьому під час нумерації кутів найменшою цифрою позначають кут трикутника, який лежить напроти сторони, що є вихідною для наступних обчислень. Інші сторони трикутників називають проміжними, напроти них лежать проміжні кути.

Зауважимо, що проблема вирівнювання виникає як для вільних так і невільних мереж. Важливою передумовою є надлишок вимірів та вихідних даних у геодезичній мережі.

2.  Спрощене зрівнювання центральної системи

Види умовних рівнянь

Умовне рівняння фігури

У трикутнику, в якого є відомі три плоскі кути, виникає умова фігури. Ця умова ставить вимогу, щоб сума плоских кутів трикутника дорівнювала 180⁰ (рис.4), тобто:

Рис. 4 Трикутник

Тут  1, 2, 3 – вирівняні кути.

Запишемо вирівняні кути 1, 2, 3 через виміряні 1', 2', 3' і поправки до них V₁, V₂, V₃, (10) тобто:

Умовне рівняння фігури (10) набуде вигляду:

1'+V₁+2'+V₂+3'+V₃-180⁰=0                      (10)

Позначимо (11):

де W_ф - вільний член умовного рівняння фігури.

Рівняння (10) запишемо (12):

Коефіцієнти за умови поправок у кути відповідно до формул системи (5) дорівнюють одиниці, тобто (13):

Умовне рівняння горизонту

Це рівняння виникає у центральній системі. Відповідна умова вимагає, щоб сума кутів, виміряних у цьому пункті по горизонту, дорівнювала 360⁰. Наприклад, для рис. 1 маємо (14):

Тут 2, 5, 8, 11 – вирівняні кути.

Запишемо їх через вирівняні кути 2', 5', 8', 11' і поправки до них V₁, V₅, V₈, V₁₁, тобто:

Умовне рівняння горизонту (14) набуде вигляду:

Позначимо (15):

де W_т – вільний член умовного рівняння фігури.

Рівняння (14) запишемо (16):

Коефіцієнти за умови поправок у кути будуть (17):

Полюсне умовне рівняння.

Полюсна умова ставить вимогу, щоб після вирівнювання значення будь-якої сторони мережі обчислювалось однозначно, незалежно від схеми обчислення.

Це рівняння виникає у центральній системі та геодезичному чотирикутнику.