Принципы моделирования сложных объектов, страница 9

Функциональная и морфологическая сложность.

Объект моделирования характеризуется тремя базовыми инвариантными атрибутами:

·  ω – организованность;

·  μ – морфология;

·  φ – поведение.

Такой объект может находится в нескольких структурных состояниях, определяемых μ и некоторых функциональных состояниях, определяемых φ.

Структурная форма объекта определяется множеством его состояний:

При определении абсолютной морфологической формы объекта используют форму «Мера Хартли»:

- это абсолютное значение сложности объекта по морфологическому показателю.

Аналогично для функциональной сложности объекта. Отличительный признак в функции: y(t)  на отрезке τ = (t_n-1, t_n), где y(t)  - непрерывная функция.

если

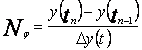
тогда

 

Для оценки текущей сложности используется оценка Шеннона:

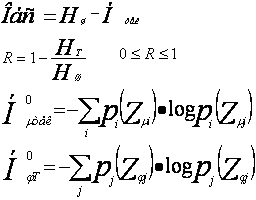
Если структурная и функциональная структуры не зависят друг от друга, то совместная сложность должна определяться произведением вероятностей: Р_μ· Р_φ. Для зависимых состояний используется формула условных Р.

Оценки сложности необходимы для сравнения различных объектов моделирования по критерию                  , а также для оценки их уровня организованности. И тот и другой показатели в итоге используются для выбора метода моделирования.

Соответствие объекта моделирования по критерию сложности.

Введем 2 шкалы:

 

Пусть объект находится на уровне сложности 6. Ставим в соответствие модель уровня 6. (модель гомоморфна объекту). Данное соответствие возможно, но совпадение по уровням практически не бывает. Если объект (модель) находится на 9 уровне, то наш сложный объект можно свести к 6 уровню модели, однако это возможно при исследовании внутренней структуры объекта. Зная принципы сложности и целостности, мы можем строить более адекватные модели.

5. Принцип соответствия модели и объекта

В модели отображается Толька та часть (компонент, аспект, свойство, процесс) объекта моделирования, которая по критериям необходимости и достаточности соответствует целям и задачам моделирования. Сложность модели и сложность объекта оригинала должны быть согласованны, это вытекает из принципа необходимости разнообразия уравнения Эшби: «Только разнообразие может уничтожить разнообразие».

Если исходить из гипотезы о нормальном распределении, то получим:

 

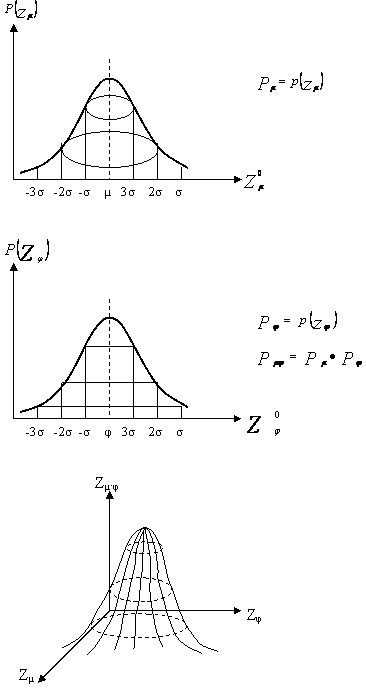Пользуясь законом «3σ» будем иметь сечения:

Проецируя все точки на плоскость Z_μ, Z_φ имеем следующий рисунок: