Принципы моделирования сложных объектов, страница 4

λ(t) = Cos α .

         Если α >0, то коэффициент уменьшается.

         При α = π / 2, λ(t) = 0.

         Т.е. имеем позитивный нейтралитет ( вектор обращается в точку при π / 2).

2.  Движение во втором квадрате. Начинается область противоречий. Цель то 0 начинает возрастать и изменяет знак (0 ÷ -1). При достижении π, коэффициент равен -1, цели достигают антогонистических отношений (антогонизм целей). Прохождение цели в верхней полуплоскости – дивергенция целей.

3.  Переход к третьей четверти дает уменьшение противоречивости: α = 3π / 2, значение λ = 0, а состояние – безразличный, негативный нейтралитет.

4.  Переход к четвертой четверти дает нам область сотрудничества, т.е. имеем целесовпадание: 0 λ +1.

5.  возвращение к позиции 1 (к 2π).

Нижняя полуплоскость означает конвергенцию, а верхняя – дивергенцию (расхождение целей). В правой полуплоскости мы имеем цели сотрудничества (конструктивные), а в левой – деструктивные (антогонистические).

Знак исходной цели (+,-) надо брать исходя их третьей цели относительно двух других. Пространство двух целей – r₂, пространство 3 цели – r₃ (объемное пространство).

Метод:

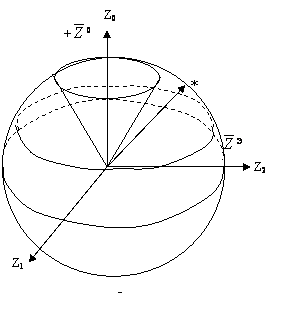
Анализ взаимодействия трех целей:

В зависимости от того, что используем в качестве внешней , задача может быть разбита на совокупность взаимосвязанных совокупных задач.

Две подзадачи ⁰⁺ и ^0- , а сам анализ задачи сводится к плоскому случаю, при условии независимости внешних Z от знака (для среза по диаметру).

Меняем внешнюю цель по конусу. Если ⁰ является для нас базой, то она остается неизменной, вертикальной, а меняются другие цели по окружности *. Движение от + к -, с увеличение угла (одна внутри другой цели начинают двигаться). Конус расширяется, затем сужается.

Полный анализ системы моделирования получим при рассмотри 3 целей: внутренней, внешней и Z³.

 

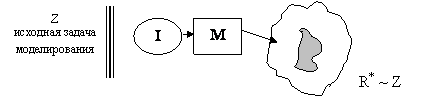
Достижение компромиссной цели. Выделим область компромиссов достижения цели.

Действительная реальная цель есть некоторый компромисс между идеальной Z и возможной степенью близости ее достижения при отдельных условиях компромисса.

   

, где   λ_ад задается в виде некоторого функционала.

- это условие адекватности, где Q_w  степень близости достижения цели.

 

- это степень достижения цели, где Т – технико, Э – экономич.

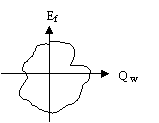
- где E_f  - эффективность.

Для анализа выбираем зоны  на осях и внутри квадратов.

 

λ_ад=0 все отношения от этой области являются компромиссами.

Эффективность (Е_f) – необходимая цена для заданного качества.

Задание. Провести анализ взаимодействия трех целей методом круговых диаграмм на сфере и анализ оценки целевой адекватности по показателям Q_w и E_f: