








Задание для студентов на практическое №1 по теме
«Основы дифференциального исчисления. Нахождение производных функций. Графики функций»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
Введение. Содержание предмета. Инструктаж по технике безопасности.
1. Производная функции. Её физический и геометрический смысл. (таблица производных основных элементарных функций)
2. Описание скорости протекания биологических процессов с помощью производной.
3. Градиенты.
4. Производные высших порядков.
5. Частные производные.
(самостоятельная подготовка)
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Примеры
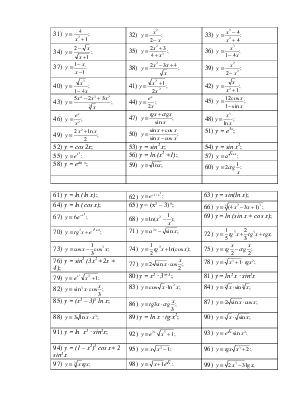
Найти производные следующих функций:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) y = xa+b; |
8) |
9) |
|
10) y = (1 – 3x2)(1 – x)3; |
11) y = (2x – 1)(x2 – 1); |
12) y = (1 – 4x3)(1 + 2x2); |
|
13) |
14) |
15) |
|
16) |
17) |
18) y = tg x – ctg x; |
|
19) y = x – sin x; |
20) y = loga x + ax; |
21) |
|
22) y = ex cos x; |
23) y = sin x ln x; |
24) y = sin x cos x; |
|
25) y = x ln x; |
26) |
27) |
|
28) y = 3 tg x ·ctg x; |
29) |
30) |
|
31) |
32) |
33) |
|
34) |
35) |
36) |
|
37) |
38) |
39) |
|
40) |
41) |
42) |
|
43) |
44) |
45) |
|
46) |
47) |
48) |
|
49) |
50) |
51) y = e3x; |
|
52) y = cos 2x; |
53) y = sin2 x; |
54) y = sin x2; |
|
55) |
56) y = ln (x2 +1); |
57) |
|
58) y = esin x; |
59) |
60) |
|
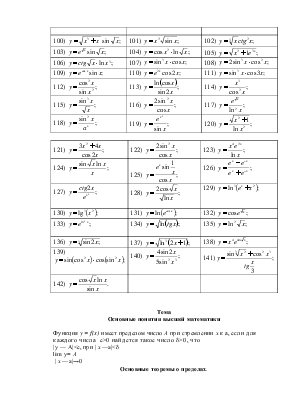
61) y = ln (ln x); |
62) |
63) y = sin(ln x); |
|
64) y = ln (cos x); |
65) y = (x2 – 3)5; |
66) |
|
67) |
68) |
69) y = ln (sin x + cos x); |
|
70) |
71) |
72) |
|
73) |
74) |
75) |
|
76) y = sin2 (3x2 +2x + 4); |
77) |
78) |
|
79) |
80) y = x2 · 3x+1; |
81) y = ln2 x · sin2x |
|
82) |
83) |
84) |
|
85) y = (x2 – 3)5 ln x; |
86) |
87) |
|
88) |
89) y = ln x · tg x2; |
90) |
|
91) y = ln x2 · sin2x; |
92) |
93) |
|
94) y = (1 – x2)3 cos x+ 2 sin2 x |
95) |
96) |
|
97) |
98) |
99) |
|
100) |
101) |
102) |
|
103) |
104) |
105) |
|
106) |
107) |
108) |
|
109) |
110) |
111) |
|
112) |
113) |
114) |
|
115) |
116) |
117) |
|
118) |
119) |
120) |
|
121) |
122) |
123) |
|
124) |
125) |
126) |
|
127) |
128) |
129) |
|
130) |
131) |
132) |
|
133) |
134) |
135) |
|
136) |
137) |
138) |
|
139) |
140) |
141) |
|
142) |
Тема
Основные понятия высшей математики
Функция y = f(x) имеет пределом число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что
|y— A|<е, при | х —a|<δ
lim y= А
| х —a|→0
Основные теоремы о пределах.
Предел постоянной величины
limА=А.
Предел суммы (разности) конечного числа функций
lim [f(x)+φ(x)+ψ(x)]= lim f(x)+ lim φ(x)+ lim ψ(x) x→а x→а x→а x→а
Предел произведений конечного числа функций
lim [f(x) •φ(x) •ψ(x)]= lim f(x) • lim φ(x) • lim ψ(x)
x→а x→а x→а x→а
Предел частного двух функций:
lim [f(x) /φ(x)]= lim f(x) / lim φ(x) при lim φ(x)≠0
x→а x→а x→а x→а
Производная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.