Итак, угловой коэффициент касательной к графику функции в данной точке равен значению ее производной в точке касания. В этом и состоит геометрический смысл производной.
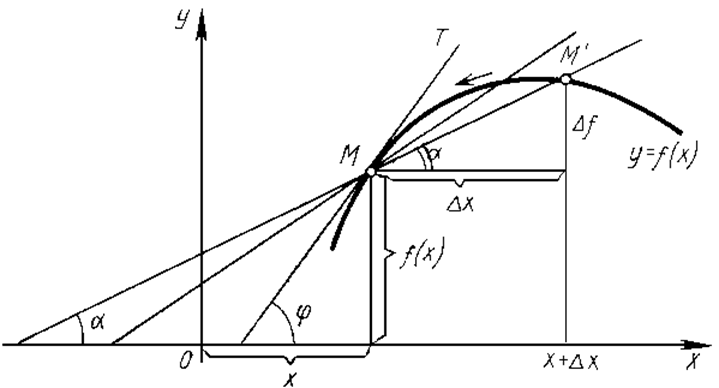
Рис. 2
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ И
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
Общее правило дифференцирования. При дифференцировании функции (нахождение ее производной) придерживаются следующие схемы:
1) выбрав некоторое значение х, дают ему приращение Dх и находят значение функции в точке х + Dх, равное f(x + Dx);
2) определяют приращение функции: Df = f(x + Dx);
3) составляют отношение Df / Dx и, если возможно, упрощают его;
4) находят производную функции, то есть предел 
(Df / Dx), если этот предел
существует: 
Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций.
.
Производная произведения двух дифференцируемых
функций равна сумме произведений второй функции на производную первой и первой
функции на производную второй: 
Производная частного (дроби) двух функций равна дроби, знаменатель которой равен квадрату знаменателя дифференцируемой функции, а числитель есть разность между произведениями знаменателя на производную числителя и числителя на производную знаменателя:
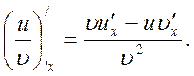
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ.
Функция у = F(x), которая числу х ставит в соответствие число f(g(x)), называется функцией от функции или сложной функцией, образованной из функций f и g в указанном порядке: у = f(g(x)), где у = f(u), u = g(x).
Например, если y = u3, u = cos x, то y = (cos x)3 = cos3 x.
Любую сложную функцию можно представить в виде элементарных функций, которые являются ее промежуточными аргументами.
Пример 1. Функция у = (х2 + 3х)2 есть сложная функция от х, так как она состоит из элементарных функций u = х2 + 3х и у = и2.
Пример 2. Функция у = sin lg(5 + 1/x3) есть сложная функция от х, так как она состоит из элементарных функций t = x3, z = 1/t, u = 5 + z, u = lg u, y = sin u.
ТАБЛИЦА ОСНОВНЫХ ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ.
1. (С)¢х = 0.
2. (х)¢х = 1.
3. (иn)¢x = nun-1u¢x; (xn)¢x = nxn-1.
4. (u + u - w)¢x = u¢x + u¢x - w¢x.
5. (uu)¢x = uu¢x + uu¢x.
6. (Cu)¢x = Cu¢x;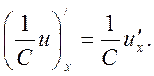 
7. 
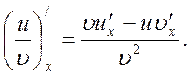
8. (au)¢x = auu¢x lna.
9. (eu)¢x = euu¢x; (ex)¢x = ex.
10. 
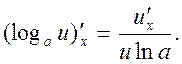
11. 
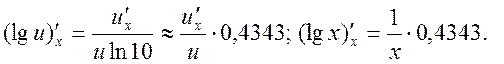
12. 
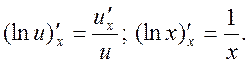
13. 
14. 
15. 
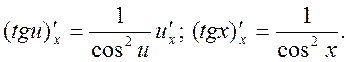
16. 
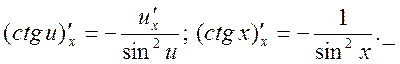
17. 
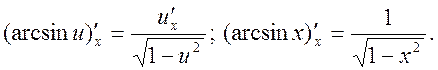
18. 
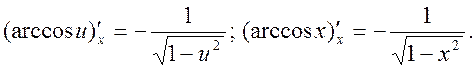
19. 
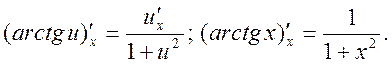
20. 
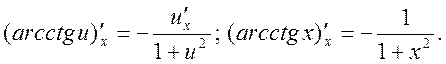
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ.
Производные второго и высших порядков. Производную f¢(x) функции у = f(x) будем называть производной первого порядка или просто первой производной этой функции. Производная функции f¢(x) является функцией от х, её можно дифференцировать .
Производная от производной называется производной второго порядка или просто второй производной.
Вторая
производная обозначается символами: 
(читается «игрек два
штриха по икс»), 
(«эф два штриха от икс»), d2y/dx2 («дэ два игрек по дэ икс дважды), d2f/dx2 («дэ два эф по дэ икс дважды»).
Исходя из
определения второй производной, можно записать: 
Вторая производная в свою очередь есть функция от х, и её можно дифференцировать.
Производная
второй производной называется производной третьего порядка или третьей
производной и обозначается 
Производная
(n – 1)-й
производной (n – натуральное число) называется производной n-го
порядка или n-й
производной и обозначается 
Например, для
функции f(x) = x5 можно найти 
и так далее.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА:
Найдите производные следующих функций:
1.
y=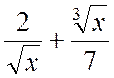
2.
у=
3. у=ln(x2+cosx)
4.
y=
Найдите дифференциалы следующих функций:
1.
y=
2.
y=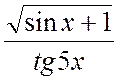
ЛИТЕРАТУРА
1. Лобоцкая Н.Л. Основы высшей математики - М.: «Вышэйшая школа», 1978. С129-164.
2. Бейли Н. Математика в биологии и медицине. Пер. с англ. М.: «Мир», 1970.
3. Ремизов А.Н., Исакова Н.Х., Максина Л.Г. Сборник задач по медицинской и биологической физике – М.: «Высшая школа», 1987. С8-15.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.