Основы дифференциального исчисления. Нахождение производных функций. Графики функций (Практическое занятие № 1), страница 2

Производной функции f(x) называется предел отношения прира-щения функции Δу к приращению аргумента Δх в точке х при стремлении Δх к нулю:

                   ý=lim (Δy /Δx) 

                       Δx →0

                        Производные некоторых функций :

у=С:	ý= 0;
y=x	ý=1
у = хμ:	ý=μxμ-1
у = аx: у = ех                 то	ý=axlna; ý= еx;
y=logax у = lпх	ý=( logae)/x=1/(x lna) ý=1/x
y=sinx y=cos x y = tgx. y = ctgx.	y'=cosx; ý = — sin x; ý =1/cos2x ý =-1/sin2x
y=arcsinx y=arccosx y=arctgx y=arcctgx	ý =1/(1-x2)1/2 ý =-1/(1-x2)1/2 ý =1/(1+x2) ý =-1/(1+x2)
y = v±u:	y' = u'±v'
y=uv	y' = u'v + v'u.
y=u/v:	y' =( u'v- v'u)/ v2
y = f1(u), если u = f2(x),	у'x = у'uu'x

ПОНЯТИЕ ПРОИЗВОДНОЙ И ЕЁ МЕХАНИЧЕСКИЙ СМЫСЛ.

          Приращение аргумента и функции. Пусть функция у=f(x) определена на некотором интервале, х₀ и х – два произвольных значения аргумента из этого интервала. Разность между двумя значениями аргумента называется приращением аргумента: х – х₀ = Dх, откуда х = х₀ + Dх, то есть значение аргумента х можно определить через х₀ и его же приращение Dх.

          Разность между двумя значениями функции называется приращением функции: Dу = Df = f(x₀ +Dx) – f(x₀).

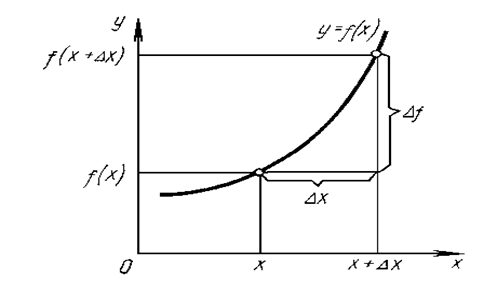
          Как видно из рис.1, приращение аргумента Dх изображается приращением абсциссы точки графика функции у = f(x), а приращение функции Df – приращение ординаты этой точки.

         

	Рис.1

 

Вычисление приращения любой функции у = f(x) удобно проводить по следующей схеме:

1)  даем аргументу х приращение Dх и получаем точку х + Dх;

2)  находим значение функции в точке х + Dх: f(x + Dx);

3)  находим приращение функции: Df = f(x + Dx) – f(x).

Понятие непрерывности. Функция f(x) называется непрерывной в точке х₀, если:

1)  функция определена в точке х₀ и в некоторой окрестности, содержащей эту точку;

2)  предел приращения функции равен нулю при стремлении приращения аргумента к нулю, то есть

                         

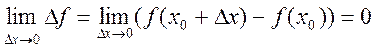
Определение производной. Задача нахождения скорости процессов привела к введению в математику понятия производной функции.

Пусть дана функция f(x), определенная на некотором интервале ]a, b[ и непрерывная на нем. Дадим аргументу  приращение Dх, тогда функция получит приращение Df:                  

     Отношение

                                            
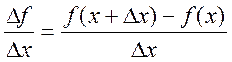
является функцией от Dх и выражает среднюю скорость изменения функции f(x) относительно аргумента х на интервале ]х, х+Dх[.

          Предел отношения Df/Dx приращения функции Df  к приращению аргумента Dх, когда Dх стремится к нулю, при условии, что этот предел существует, называется производной функции f(x) в точке .

          Таким образом, можно сделать следующий вывод: производная функции y = f(x):

                                                          

В этом и состоит физический (в том числе механический) смысл производной.

          Процесс нахождения производной называется дифференцированием, поэтому выражение «продифференцировать функцию» равносильно выражению «найти производную функции».

           ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.

 По уравнению непрерывной линии у = f(x) найдем угловой коэффициент касательной к ней в данной точке М(х; f(x)), предполагая, что касательная существует.

          Функция y = f(x) в прямоугольной системе координат изображается кривой (рис.2). Возьмем на кривой точку М(х; f(x)) и дадим аргументу х приращение Dх. По значению аргумента х+Dх получаем новое значение функции f(x + Dx), соответствующее точке М¢(х +Dх; f(х + Dх)) на кривой. Проведем секущую ММ¢ и обозначим угол наклона секущей к оси Ох через a. Из рисунка следует, что Df/Dx=tga. При Dх ® 0 точка М¢ перемещается вдоль кривой, приближаясь к точке М. Секущая ММ¢ поворачивается вокруг точки М, и величина угла a изменяется. При приближении секущей ММ¢ к касательной МТ угол a приближается к углу j  и

       

Угловой коэффициент касательной