Тригонометрический ряд и его основные свойства. Ряд вида
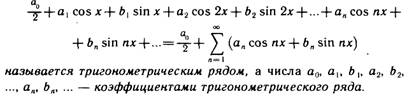 |
В отличие от степенного ряда, в тригонометрическом ряде вместо простейших функций х, х2, ..., хп, ... взяты тригонометрические функции
1/2, cos x, sin x, cos 2x, sin 2x,
..., cos nx, sin nx, ... (2.1)
Прежде всего отметим, что все функции системы (2.1) являются периодическими с периодом 2π. Поэтому и любая частичная сумма ряда 2π-периодична. Отсюда следует, что если ряд сходится на отрезке [-π, π], то он сходится на всей числовой прямой и его сумма, будучи пределом последовательности периодических частичных сумм, является периодической функцией с периодом 2л. Поэтому тригонометрические ряды особенно удобны при изучении периодических функций, описывающих различные периодические процессы.
Другим важным свойством функций системы (2.1) является их ортогональность на отрезке [ - π, π].
Ряд Фурье. Аналогично степенному ряду, для тригонометрического ряда имеет место следующая теорема.
ТеоремаЕсли функция f (x) определена и интегрируема на отрезке [ - π, π], разлагается в тригонометрический ряд
который можно интегрировать почленно, то это разложение единственно.
Для функций нечетных на отрезке [ - π, π], коэффициенты bk=0, а для четных на том же отрезке ak=0.
![]() Пример. Рассмотрим функцию f(x) = x. Эта функция может быть разложена в ряд
Фурье. Так как она нечетная, то ее коэффициеты Фурье a=0, а b находятся по формуле:
Пример. Рассмотрим функцию f(x) = x. Эта функция может быть разложена в ряд
Фурье. Так как она нечетная, то ее коэффициеты Фурье a=0, а b находятся по формуле:
Таким образом, получаем ряд Фурье данной функции
Это равенство справедливо для любого х в [ - π, π]. В точках x=± π сумма ряда Фурье не совпадает со значениями функции f(x)=x, а равна нулю. Вне отрезка [ - π, π] сумма ряда является периодическим продолжением функции f(x)=x график изображен на рис.2.1.
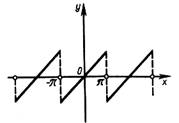 |
Рис.2.1.
В случае, если функция f(x) определена на отрезке [-l,l], (l- произвольное положительное число), имеет период 2l и может быть разложена в ряд Фурье, то выражение для ряда примет следующий вид:
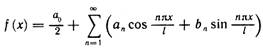 |
|||
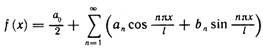 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.