Тригонометрический ряд и его основные свойства, страница 2

Пример. Разложить в ряд Фурье с периодом 2 l функцию f (x), которая на отрезке [ - l, l] задается формулой f(х)=|x|. Решение:

Так как функция f (x)=|x| четная, то

 

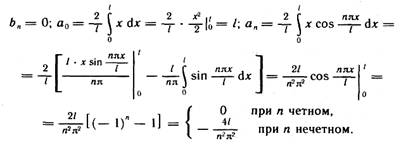Следовательно, ряд Фурье функции f (х) имеет вид

  

На рис.2.1 приведена схема подразделения основных видов встречающихся на практике сигналов, каждая категория из которой обычно требует специальных методов измерения и анализа.

 

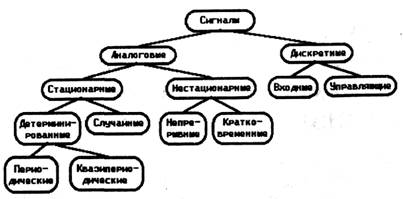Рис.2.1.

Первые две большие группы в данной классификации образуют ана­логовые и дискретные сигналы. Аналоговые сигналы характеризуют­ся возможностью изменения своих амплитуд в потенциально непре­рывном континууме значений. В отличие от этого дискретные сигна­лы принимают значения только из некоторого конечного множества (коды) или же только два значения типа Да или Нет (бинарные сиг­налы). Дискретные сигналы обычно несут информацию о некоторых событиях в окружающей среде (и тогда они играют роль входных сигналов) или же они генерируются контроллером для выполнения управляющих действий во внешней среде (тогда они являются вы­ходными для контроллера).

В свою очередь аналоговые сигналы на своем верхнем уровне под­разделяются на стационарные и нестационарные. Стационарными в практических приложениях можно считать процессы, средние зна­чения и дисперсия которых не изменяются во времени и не зависят от используемой при их определении реализации. Это справедливо как для детерминированных, так и для случайных сигналов, хотя в случае случайных сигналов результаты обработки различных реали­заций могут и не быть идентичными.

Мгновенное значение стационарного детерминированного сигнала может быть предсказано для любого момента времени, а для ста­ционарных случайных сигналов можно определить лишь присущие им статистические параметры: средние значения, моменты, диспер­сию и т.п.

Детерминированные сигналы содержат только синусоидальные со­ставляющие с дискретными частотами. В случае периодических сиг­налов (рис. 2.2а) все эти дискретные частоты являются кратными основной частоты. Дискретные частоты спектральных составляющих квазипериодических сигналов (рис. 2.2б) связаны друг с другом не гармоническими, а иррациональными соотношениями. Однако встречающиеся на практике квазипериодические сигналы обычно созданы путем смешивания двух или больше независимых групп гармоник (например, генерируемых путевым генератором сигналом частотой 50 Гц и силовой линией электроснабжения с той же частотой).

 

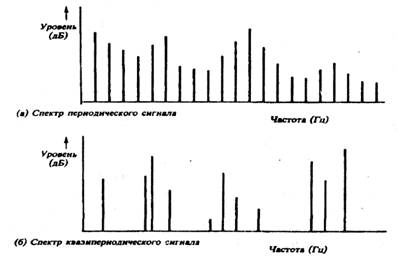Рис.2.2.

На практике часто заранее известно вероятное расположение со­ставляющих анализируемого сигнала (например, гармоник частоты вращения определенной детали машины, гармоник частоты сети пе­ременного тока и др.).

Случайные стационарные сигналы, в отличие от детерминирован­ных, имеют непрерывные спектры (рис. 2.3), но и в этом случае обычно заранее известны вероятное расположение и ширина пиков спектра анализируемого сигнала.