Тригонометрический ряд и его основные свойства, страница 3

Пример непрерывного спектра стационарного случайного

сигнала

 

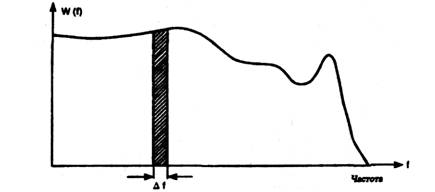Рис.2.3.

Например, пики спектров случай­ных сигналов часто созданы путем фильтрации широкополосных случайных сигналов физическими системами, имеющими резонансы с определенными значениями коэффициента добротности Q (т.е. коэффициента усиления в области резонанса). Значения этого коэф­фициента часто связаны с параметрами используемых материалов, конструкцией и т.д., поэтому могут быть заранее предсказаны. Более того, ввиду обратной пропорциональности коэффициента добротно­сти Q к относительной (процентной) ширине резонансного пика также можно предсказать приблизительную ширину пиков спектров анализируемых случайных сигналов.

Хотя спектры мощности случайных процессов могут быть довольно точно определены, присущие им спектры фазы имеют случайный ха­рактер и обычно вообще не интересны при анализе изолированных и несвязанных друг с другом случайных сигналов. Однако, при одно­временном анализе нескольких случайных сигналов, в частности при анализе взаимосвязанных сигналов, нужно определять фазовые от­ношения между несколькими спектрами.

Несмотря на невозможность предсказания мгновенных значений, свойства случайных сигналов можно описать статистически при по­мощи функций плотности вероятности и распределения вероятно­стей.

Псевдослучайными называются специальные периодические сигна­лы, используемые для имитационного моделирования случайных сиг­налов. Хотя эти сигналы и являются периодическими, но их период Т весьма длителен, так что присущие им спектральные составляю­щие расположены на малых 1/Т расстояниях друг относительно друга (рис.2.4). Фазовые соотношения смежных составляющих этих сигналов являются случайными, следовательно, передача псевдослучайных сигналов линейной физической системой с резонансами почти идентична передаче аналогичных случайных сигналов. Плот­ность вероятности псевдослучайных сигналов может довольно точно соответствовать закону Гаусса.

Пример спектров амплитуды и фазы псевдослучайного сиг­нала

 

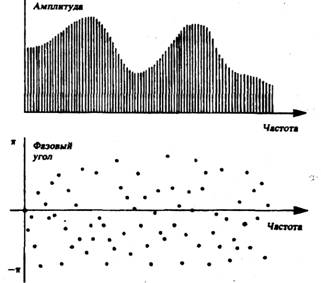Рис.2.4.

Большое преимущество псевдослучайных сигналов заключается в возможности их точного воспроизведения, что особенно ценно с точки зрения стандартизации разного рода испытаний. Однако при этом нужно помнить, что псевдослучайные сигналы являются перио­дическими сигналами. Это сказывается на идентичном возбуждении нелинейных систем и на потери присущей случайным сигналам точ­ности линейной аппроксимации.

Нестационарные сигналы могут быть подразделены на две группы: непрерывные нестационарные сигналы (например, речь) и кратко­временные сигналы, амплитуда которых в начале началу и конце измерения равна нулю, поэтому они обрабатываются и анализиру­ются в целом, в то время как непрерывные нестационарные сигналы (которые на практике также имеют начало и конец в реальном вре­мени) подвергаются обработке и анализу по участкам, в которых они обычно имеют характер квазистационарных сигналов.

Хотя наименование нестационарные можно отнести ко всем сигна­лам, которые не удовлетворяют требованиям стационарности, но общим свойством большинства практических нестационарных сигна­лов является то, что их можно подразделить на участки, в которых они имеют характер квазистационарных сигналов. Например, непре­рывную речь можно подразделить на короткие звуки (гласные звуки, согласные звуки и т.д.). Характерным отличием кратковременных сигналов является то, что их амплитуда в начале и в конце равна нулю.