Дифференциал функции (Практическое занятие № 2)

Задание для студентов на практическое №2 по теме

«Дифференциал функции»

Цель занятия: Научиться решать примеры и задачи по данной теме

Вопросы теории ( исходный уровень)

1.  Применение производных для исследования функций на экстремум.

2.   Дифференциал функции, его геометрический и физический смысл.

3.  Полный дифференциал функции многих переменных. 

4.  Состояние организма как функция многих переменных.

5.  Приближенные вычисления.

6.  Нахождение частных производных и полного дифференциала.

7.  Примеры использования указанных понятий в фармако­кинетике, микробиологии и др.

(самостоятельная подготовка)

Содержание занятия:

1.ответить на вопросы по теме занятия

2.решить примеры

Примеры

Найти дифференциалы следующих функций:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

Тема

Применение производных для исследования  функций

Условие возрастания функции y = f(x) на отрезке [а, b]

f'(x)>0

Условие убывания функции y=f(x) на отрезке [а, b]

f'(x)<0

Условие максимума функции y=f(x) при x= а

f'(a)=0 и f'' (a)<0

Если при х=а производные f'(а) = 0 и f"(а) = 0, то необходи­мо исследовать f'(x) в окрестностях точки x = а. Функция у=f(х) при х=а имеет максимум, если при переходе через точку х= а производная f'(x) меняет знак с «+» на «-», в случае минимума — с « - » на «+» Если f'(x) не меняет знака при переходе через точку х = а, то в этой точке у функ­ции экстремума нет

Дифференциал функции.

Дифференциал независимой переменной  равен ее приращению:

dx=Δx

Дифференциал функции y=f(x)

  dy = у' Δх.

Дифференциал суммы  (разности) двух функций y=u±v

dy=du±dv.

Дифференциал произведения двух функций у=uv

dy = vdu-\-udv.

Дифференциал частного двух функций y=u/v

dy=(vdu-udv)/v²

   Приращение функции

Δy = f(x + Δx) - f(x) ≈ dy ≈ f'(x) • Δx

где Δx: — приращение аргумента.

Приближенное вычисление значения функции:

f(x + Δx)  ≈ f(x) + f'(x) • Δx

Применениедифференциала  в  приближенных  вычислениях

Дифференциал применяется для вычисления абсолютной и отно­сительной погрешностей при косвенных измерениях u = f(x, у, z .). Абсолютная погрешность результата измерения

du≈Δu≈|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…

Относительная погрешность результата измерения

du/u≈Δu/u≈(|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…)/u

ДИФФЕРЕНЦИАЛ ФУНКЦИИ.

            Дифференциал функции как главная часть приращения функции. С понятием производной тесно связано понятие дифференциала функции. Пусть функция f(x) непрерывна при данных значениях х и имеет производную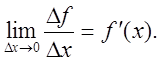

            Df/Dx = f¢(x) + a(Dx), откуда приращение функции Df = f¢(x)Dx + a(Dx)Dx, где a(Dх) ® 0 при Dх ® 0. Определим порядок бесконечно малой f¢(x)Dx по отношению к бесконечно малой Dх.:

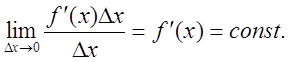
            Следовательно, бесконечно малые f¢(x)Dx и Dx имеют одинаковый порядок  малости, то есть f¢(x)Dx = O[Dx].

            Определим порядок бесконечно малой a(Dх)Dх по отношению к бесконечно малой Dх:

                                   

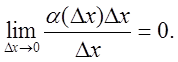
            Следовательно, бесконечно малая a(Dх)Dх имеет более высокий порядок малости по сравнению с бесконечно малой Dх, то есть a(Dх)Dх = о[Dх].

            Таким образом, бесконечно малое приращение Df  дифференцируемой функции может быть представлено в виде двух слагаемых: бесконечно малой f¢(x)Dx одинакового порядка малости с Dх и бесконечно малой a(Dх)Dх более высокого порядка малости по сравнению с бесконечно малой Dх. Это означает, что в равенстве Df=f¢(x)Dx + a(Dx)Dx  при Dх® 0 второе слагаемое стремится к нулю «быстрее», чем первое, то есть a(Dх)Dх = о[f¢(x)Dx].

            Первое слагаемое f¢(x)Dx, линейное относительно Dх, называют дифференциалом функции f(x) в точке х и обозначают dy или df  (читается «дэ игрек» или «дэ эф»). Итак,

                                               dy = df = f¢(x)Dx.

            Аналитический смысл дифференциала заключается в том, что дифференциал функции есть главная часть приращения функции Df, линейная относительно приращения аргумента Dx. Дифференциал функции отличается от приращения функции на бесконечно малую более высокого порядка малости, чем Dx. Действительно, Df=f¢(x)Dx + a(Dx)Dx  или  Df = df + a(Dx)Dx.    Дифференциал аргумента dx равен его приращению Dx: dx=Dx.

Пример. Вычислить значение дифференциала функции f(x) = x³ + 2x,  когда х изменяется от 1 до 1,1.

            Решение. Найдем общее выражение для дифференциала этой функции:

                                         

            Подставляя значения dx=Dx=1,1–1= 0,1 и x = 1 в последнюю формулу, получим искомое значение дифференциала: df½_x=1; = 0,5.                                                                                                                   

 ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ.

Частные производные первого порядка. Частной производной первого порядкафункции z = f(x,y) по аргументу х в рассматриваемой точке (х; у) называется предел

                                   

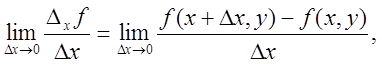
если он существует.

            Частная производная функции z = f(x, y) по аргументу х обозначается одним из следующих символов:

            Аналогично частная производная по у обозначается  и определяется формулой:

                                   

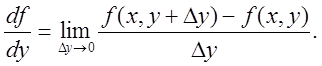
          Так как частная производная – это обычная производная функции одного аргумента, то ее нетрудно вычислить. Для этого нужно пользоваться всеми рассмотренными до сих пор правилами дифференцирования, учитывая в каждом случае, какой из аргументов принимается за «постоянное число», а какой служит «переменной дифференцирования».

            Замечание. Для нахождения частной производной, например по аргументу х – df/dx, достаточно найти обыкновенную производную функции f(x,y), считая последнюю функцией одного аргумента х, а у – постоянной; для нахождения df/dy – наоборот.

            Пример. Найти значения частных производных от функции f(x,y) = 2x²+ y² в точке Р(1;2).

            Решение. Считая f(x,y) функцией одного аргумента х и пользуясь правилами дифференцирования, находим

           

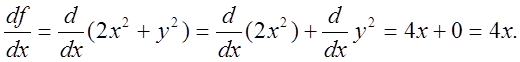
            В точке Р(1;2) значение производной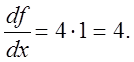        

            Считая f(x;y) функцией одного аргумента у, находим

                                             

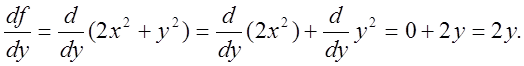
            В точке Р(1;2) значение производной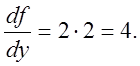

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА:

Найдите дифференциалы следующих функций:

1. y=
2. y=

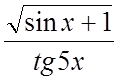
Решить следующие задачи:

1.  На сколько уменьшится площадь квадрата со стороной х=10см, если сторону уменьшить на 0,01 см?

2.  Дано уравнение движения тела: y=t³/2+2t², где s – выражено в метрах, t-в секундах. Найти путь s, пройденный телом за t=1,92 с от начала движения.

 ЛИТЕРАТУРА

1.  Лобоцкая Н.Л. Основы высшей математики - М.: «Вышэйшая школа», 1978.C198-226.

2.  Бейли Н. Математика в биологии и медицине. Пер. с англ. М.: «Мир», 1970.

3.  Ремизов А.Н., Исакова Н.Х., Максина Л.Г. Сборник задач по медицинской и биологической физике – М.: «Высшая школа», 1987. С16-20.