21. Составление уравнений типовых процессов механообработки. Ортогональное точение деталей типа «вал» (задача с двумя степенями свободы).
В общем случае при осуществлении движения подачи инструмента в технологической системе:
• появляются силы, вызывающие деформации;
• детали системы в процессе резания стремятся вернуться в свое исходное состояние, преодолевая при этим силы сопротивления вязкой среды.
Наличие масс и нелинейностей усложняют рассмотрение протекания процесса, однако, как выяснилось, влиянием масс можно в ряде случаев пренебречь. При этом условии процесс в основном определяется упругими деформациями и вязким трением.
При оценке динамических свойств системы в качестве входной величины удобно рассматривать подачу режущего инструмента.
Выходной величиной могут быть различные перемещения, что подсказывается удобством встраивания первичного чувствительного элемента - датчика.
В случае обработки вала на токарном станке при отсчете входной и выходной величины от одной и той же базы, например, относительно станины станка можно отметить, что если бы система была статична (т. е. не происходило бы резания), то для подачи резцедержателя на величину хвх потребовалась бы сила Fвх, пропорциональная этому перемещению для преодоления упругих сил, развиваемых в результате изгиба резца с жесткостью j2.
Жесткость детали несоизмеримо больше, и поэтому полагаем, что (j1 = ∞) - Fвх = j2 хвх.
Для любого момента времени, вследствие динамики явления, сила, вызывающая деформирование резца, оказывается пропорциональной величине
у1 = хвх — yвых,
являющейся стрелой прогиба резца, закрепленного как консоль.
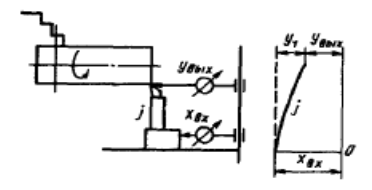
Для любого момента времени к резцу приложена сила:
Ft = j2 у1 = j2 (хвх — yвых).
Силой, направленной в обратном направлении, является прежде всего сила резания, пропорциональная при прочих равных условиях производной от величины увых:
Р = Cdyвых /df,
где С — коэффициент пропорциональности, значение которого подлежит дальнейшему уточнению; yвых — текущая величина.
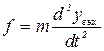 В системе действует и сила инерции, обусловленная
наличием некоторой массы - приведенной массы системы «резец —
резцедержатель» т:
В системе действует и сила инерции, обусловленная
наличием некоторой массы - приведенной массы системы «резец —
резцедержатель» т:
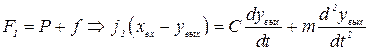 где yвых — текущая
величина.
где yвых — текущая
величина.
Уравнение сил в общем виде:
При токарной обработке осевая сила (датчики контролируют перемещения в осевом направлении):
![]()
Приняв, что,
•
![]()
![]() ;
;
• продольная подача на оборот детали ;
•
![]() приняты
постоянные, определяемые режимом обработки, материалами детали и резца и
другими условиями;
приняты
постоянные, определяемые режимом обработки, материалами детали и резца и
другими условиями;
•
![]() , где К —
некоторая постоянная величина,
, где К —
некоторая постоянная величина,
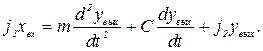 |
получаем из уравнения сил следующее выражение:
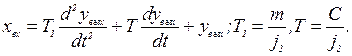 |
После деления на j2 и преобразований получаем:
Полученное дифференциальное уравнение указывает на то, что рассматриваемая технологическая система представляет собой звено второго порядка.
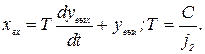 Это теоретически означает возможность появления затухающего
колебательного переходного процесса, но на практике вследствие малости
приведенной массы т и иногда возникающих незначительных ускорений
величиной
Это теоретически означает возможность появления затухающего
колебательного переходного процесса, но на практике вследствие малости
приведенной массы т и иногда возникающих незначительных ускорений
величиной ![]() вполне можно пренебречь.
вполне можно пренебречь.
Уравнение движения поэтому может быть переписано так:
Это указывает на возможность представления рассматриваемой технологической системы как некоторого апериодического звена с передаточным коэффициентом
К = 1 и постоянной времени Т = С/ j2.
В зависимости от связи колебательных систем узлов станка, механизма главного движения и механизма движения подач детали могут колебаться независимо друг от друга или оказывать влияние друг на друга.
Для того чтобы станок работал точно и его колебания были минимальны, следует решать систему «станок—приспособление—инструмент—заготовка» так, чтобы статические и динамические изменения в измерительных звеньях были такими же, как и между инструментом и заготовкой.
Допустимое значение этой разности определяют исходя из заданной геометрической и рабочей точности и динамической устойчивости станка в зависимости от положения инструмента и заданной мощности резания.
На основании этого определяют необходимую статическую и динамическую жесткость станка.
Рассмотрим, например, методику определения вынужденных колебаний плоскошлифовального станка.
Введем допущение: заготовка обладает бесконечно большей жесткостью по сравнению с жесткостью шлифовального круга.
Определяем силовые воздействия и (t) на заготовку дисбаланса шлифовального круга и изменение yt (t) глубины резания вследствие эксцентриситета круга.
В данном случае станок можно представить в виде системы с одной степенью свободы, где переменной состояния является величина q (t) относительно положения шлифовального круга и заготовки.
На
основании принципа Даламбера поведение системы описывает система обычных
дифференциальных уравнений вида: 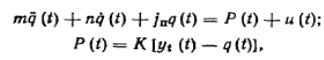
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.