Составление уравнений типовых процессов механообработки. Ортогональное точение деталей типа «вал» (задача с двумя степенями свободы). Устойчивость линейных непрерывных САР. Поведение свободной (переходной) составляющей при попарно сопряженных комплексных, чисто мнимых и нулевых корнях характеристического уравнения, страница 2

где m — приведенная масса; n — коэффициент демпфирования; j_п — жесткость подсистемы; Р (t) — изменение силы резания;

K— коэффициент пропорциональности.

Преобразуем данную систему уравнений к следующему виду:

 

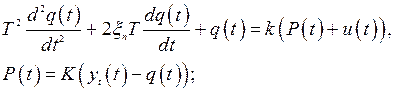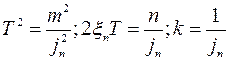При разработке модели процесса ортогонального точения примем следующие допущения.

1. Будем считать, что процесс обработки можно представить в виде простейшей линейной упругой системы с двумя степенями свободы, схема которой представлена ниже.

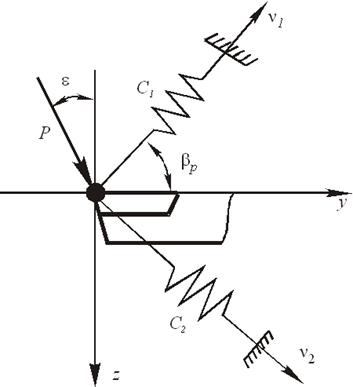2. Смещение резца у, являющееся выходным параметром,

связано с координатами ν₁ и ν₂ зависимостью:

y = ν₁cos(ε + β_p) – ν₂sin(ε + β_p).

3. Смещение элемента системы в направлении

выдерживаемого размера – глубины резания зависит

от сопротивления элемента внешнему силовому

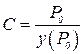воздействию, которое в целом характеризуется

коэффициентом жесткости элемента:

Приняты следующие обозначения.

С₁, С₂ – жесткости системы по главным осям жесткости.

Р – эквивалентная сила, воздействующая на систему:

P = ξP_z + ηP_y + γP_x,

где ξ, η, γ - коэффициенты, характеризующие степень

Влияния каждой составляющей силы резания Р.

Вынужденные колебания системы «резец – суппорт» в первом приближении можно

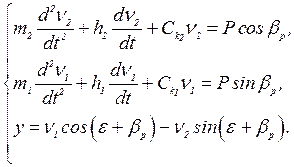описать следующей системой уравнений:

Здесь m₁, m₂ – приведенные массы данной системы; h₁, h₂ – коэффициенты сил сопротивления;                            

             - главные жесткости системы.

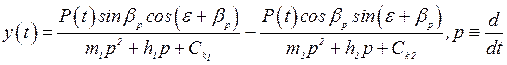Решая данную систему в операторной форме получаем следующее общее выражение для смещения резца у в любой момент времени t:

Передаточные функции рассмотренных процессов механообработки

1. Одномерная система, моделирующая ортогональное точение.

 

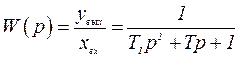Передаточная функция в операторной форме:

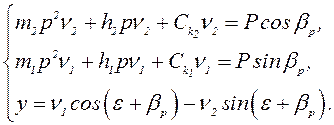2. Двухмерная система, моделирующая ортогональное точение.

Передаточная функция системы, моделирующей отжатие резца при точении, в операторной форме:

 

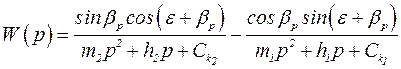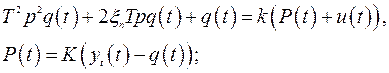3. Одномерная система, моделирующая плоское шлифование.

 

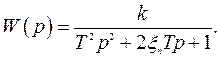Передаточные функции в операторной форме:

Механическая система шлифования на центрах представлена ниже.

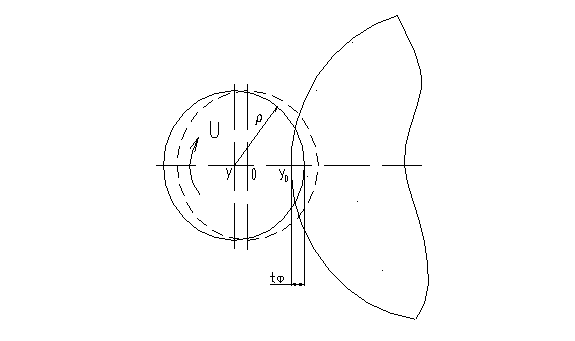
В качестве допущения принимается, что жесткость шлифовальной бабки абсолютна.

Начало координат совмещается с осью вращения заготовки.

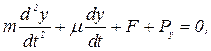Учитывая, что в системе имеет место жидкостное трение, уравнение движения заготовки можно записать в виде:

где m - приведенная масса подвижной системы, μ- коэффициент демпфирования, F - радиальная составляющая реакции центров в сопряжении с заготовкой, P_y - радиальная составляющая силы резания.

Для случая обработки вблизи одного из центров реакция может быть представлена следующим образом: F = jy, где j - жесткость сопряжения «центр – заготовка».

При нагружении радиальной силой отжатия заготовки в сечении центрового отверстия не постоянны, а изменяются при повороте ее на центрах. Причина этого - в погрешности формы центрового отверстия.

Центровые отверстия, как правило, на установочной поверхности имеют ряд выступов и впадин.

При установке изделия в центрах контакт между установочной поверхностью центрового отверстия и центром осуществляется по указанным выступам.

В таких условиях наибольшая величина отжатия соответствует впадине, наименьшая - выступу на поверхности центрового отверстия, т. е. эпюра отжатий повторяет форму центрового отверстия.

Наибольшей величине отжатия соответствует наименьшая жесткость, наименьшей - наибольшая жесткость сопряжения «центр – заготовка».

Поэтому жесткость сопряжения «центр – заготовка» может быть представлена как:

 

Здесь j₀ - постоянная составляющая жесткости, j_max и j_min - соответственно  максимальное  и  минимальное значения жесткости, k - число волн на центровом отверстии заготовки, ω - циклическая частота вращения заготовки, τ - время.