Составление уравнений типовых процессов механообработки. Ортогональное точение деталей типа «вал» (задача с двумя степенями свободы). Устойчивость линейных непрерывных САР. Поведение свободной (переходной) составляющей при попарно сопряженных комплексных, чисто мнимых и нулевых корнях характеристического уравнения, страница 3

Учитывая последнюю зависимость, реакция центров определяется следующим образом:

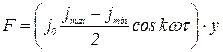Из теории резания известно, что Р_у характеризуется зависимостью:

Согласно рисунку фактическая глубина резания t_ф равна:

t_ф = y + ρ – y₀; ρ = ρ₀ + ρ(t),

где ρ - текущий радиус шлифуемой шейки, y₀ - координата, соответствующая настроечному размеру; ρ(t) - переменная составляющая радиуса; ρ₀ - среднее значение радиуса заготовки. 

Переменная составляющая может быть представлена рядом Фурье.

Первая гармоника этого ряда характеризует собой эксцентриситет профиля относительно номинального центра, а последующие - форму дополнительных замкнутых кривых, симметричных относительно этого центра.

Обычно удается отчетливо выделить лишь одну гармонику, соответствующую погрешности, которую имела шейка перед шлифованием. В таких случаях можно записать:

где Н - амплитуда волны, p - число волн на поверхности шейки, δ - сдвиг по фазе относительно эпюры жесткости.

Выходная величина, которая характеризует точность формы поперечного сечения обработанной детали, связана не со смещением координаты оси заготовки y₁, а с

изменениями этого смещения ξ = y – y₁ →                   .

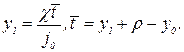В идеальном случае координата оси заготовки y₁ при ρ = ρ₀ = constи y = y₀ = const равна:

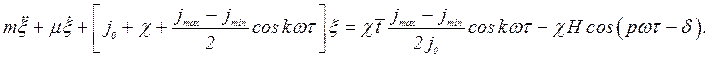Подставляя полученные выражения в уравнение сил, получаем:

В правой части уравнения присутствуют переменные возмущающие силы, которые в установившемся режиме приводят к возникновению вынужденных колебаний, а в левой части присутствует изменяющийся параметр самой системы                            , который может вызвать параметрические колебания.

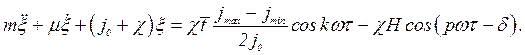В практике же шлифовальных работ основную роль играют вынужденные колебания, поэтому можно принять, что «движение» системы при шлифовании в центрах, описывается уравнением:

Для установившегося режима (статического равновесия) решение данного уравнения имеют вид:

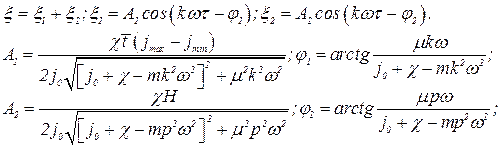Величина                                   описывает погрешность формы поперечного сечения детали, обусловленную непостоянством жесткости сопряжения «центр – заготовка», т.е. обработанная деталь наследует погрешность формы центровых отверстий.

Величина                                   описывает погрешность формы поперечного сечения детали, обусловленную погрешностью формы исходной заготовки.

22. Устойчивость линейных непрерывных САР. Теоремы А.М. Ляпунова. Поведение свободной (переходной) составляющей при вещественных и различных корнях характеристического уравнения.

23. Устойчивость линейных непрерывных САР. Поведение свободной (переходной) составляющей при попарно сопряженных комплексных, чисто мнимых и нулевых корнях характеристического уравнения.

Устойчивость – это свойство САУ возвращаться в состояния покоя или установившегося  движения, из которого  система  была выведена каким-либо воздействием после устранения этого воздействия.

Обычно понятие  устойчивости иллюстрируется следующими примерами.

Будем считать системой некоторый шар, который может находиться в одном из трех состояний:

а). Устойчивое состояние системы. б). Неустойчивое состояние системы. в). Нейтрально – устойчивое

                                                                                                                                    состояние системы.

Из решения обыкновенного дифференциального уравнения, описывающего динамику линейной САУ, переходной процесс будет затухать, если с течением времени свободная составляющая будет стремиться к нулю:

или в противном случае, при расходящемся процессе: