Составление уравнений типовых процессов механообработки. Ортогональное точение деталей типа «вал» (задача с двумя степенями свободы). Устойчивость линейных непрерывных САР. Поведение свободной (переходной) составляющей при попарно сопряженных комплексных, чисто мнимых и нулевых корнях характеристического уравнения, страница 5

С течением времени t свободная составляющая увеличивается и амплитуда выходной переменной y(t) возрастает, т.е. линейная система является неустойчивой.

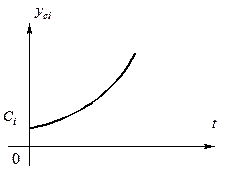
Свободная составляющая при                              Свободная составляющая при положительном

отрицательном вещественном корне                                       вещественном корне

2. Корни комплексные попарно сопряженные

2.1 Корни комплексно-сопряженные с отрицательной вещественной частью:

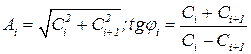
                                                                                          , где

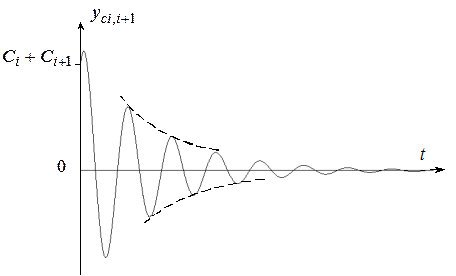
Свободная составляющая представляет собой затухающие гармонические колебания, амплитуда которых определяется вещественной частью α , а частоты (период) мнимой β.

2.2 Корни комплексно-сопряженные с положительной вещественной частью:

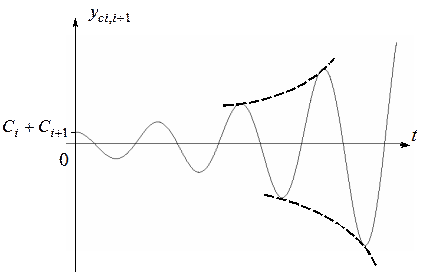
Свободная составляющая будет представлять собой гармонический сигнал, который с течением времени будет возрастать по амплитуде в соответствии с экспоненциальным законом, в результате чего линейная непрерывная САУ становится неустойчивой.

3. Корни чисто мнимые.

Здесь А, φ  – амплитуда и фазовый сдвиг соответственно, зависящие при ненулевых начальных условиях от C_i и C_i+1.

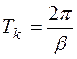Свободная составляющая представляет собой незатухающие автоколебания, период которых определяется как

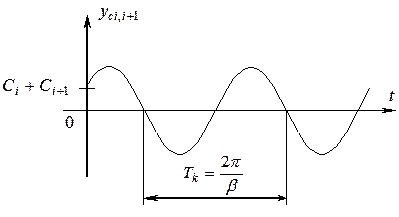
Такой режим работы линейной непрерывной САР, при котором на выходе имеет место незатухающий гармонический сигнал, соответствует границе устойчивости.

4. Корни нулевые.

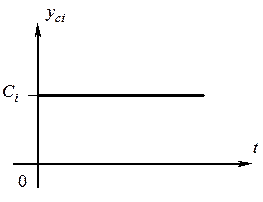
Свободная составляющая не изменяется в переходном процессе и определяется постоянной интегрирования C_i.

Наличие одного нулевого корня свидетельствует об отсутствии свободного члена a_n в однородном дифференциальном уравнении:                                                                               , которое в данном случае будет иметь следующий вид:

В данной ситуации система анализируется на устойчивость применительно к первой производной py  выхода  и является независимой (нейтральной) относительно выходной переменной y.

Определение. САУ с нулевым корнем при остальных с отрицательной вещественной частью является нейтрально устойчивой.

 Для устойчивости линейной непрерывной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть.

Обобщая рассмотренные случаи можно заключить:

- если в характеристическом уравнении D(p) имеется хотя бы один корень с положительной вещественной частью, то линейная непрерывная САУ является неустойчивой;

- если среди всех корней D(p)  с отрицательной вещественной частью присутствует пара чисто мнимых, то САУ находится на границе устойчивости;

- если характеристическое уравнение D(p) имеет один или несколько нулевых корней при остальных с отрицательной вещественной частью, то САУ является нейтрально устойчивой.

Определение. Параметры линейной системы, такие как коэффициенты передачи или демпфирования, постоянные времени и т.д., при которых САУ находится на границе устойчивости, называются граничными (критическими).

Для графической иллюстрации устойчивости используют комплексную плоскость, на которой откладывают корни характеристического уравнения (корневой портрет).

Для устойчивости линейной системы необходимо и достаточно, чтобы корни       располагались слева от мнимой оси.

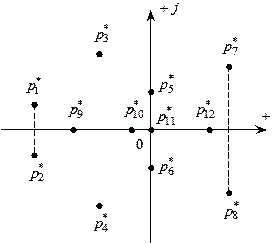
Если корни D(p) находятся справа от мнимой оси (                  ), то САУ неустойчива.

При наличии пары чисто мнимых корней             , а остальных “левых”, система находится на границе устойчивости, а при нулевом корне        САУ является нейтрально устойчивой. Причем, более удаленным корням от мнимой оси соответствуют более быстрые моды  в

свободной составляющей