Чтобы получить фазовый сдвиг 90° между напряжениями 
и 
, одно из них, 
,
подается на вход фазовращателя ФВ, в результате чего на входы сумматора А5 поступают
напряжения Uc и jUs. Выходное напряжение
сумматора А5, являющееся выходным напряжением калибратора фазы, описывается
соотношением (*).
Фаза 
определяется
управляющим кодом, а амплитуда выходного напряжения зависит только от амплитуды
входного напряжения Uвх (в рассмотренном случае Uвых=Uвх).
Разность между расчетными и заданными значениями фазы и амплитуды выходного напряжения будет тем меньше, чем точнее моделируются функциональные зависимости cosx и sinx.
Функции cosx и sinx могут быть представлены в виде суммы степенного ряда, причем тем точнее, чем больше членов степенного ряда при этом используется и чем меньше диапазон изменения аргумента x. Когда заданы число членов ряда и диапазон изменения переменной x, задача минимизации погрешности моделирования сводится к точному вычислению коэффициентов при суммирующихся членах ряда.
В табл. 1 приведены значения коэффициентов an, рассчитанные для трех случаев, когда высшая степень x и число ЦАП в схеме калибратора фазы соответственно равны семи, шести и пяти.
Методическая фазовая погрешность и нестабильность амплитуды выходного напряжения определяются соотношениями
.
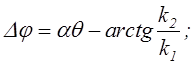
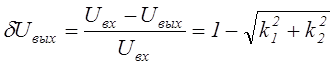Графики этих зависимостей приведены на рис. 6. (а, б) (где m - число ЦАП в схеме), а их максимальные значения указаны в табл.2.
Таблица 2.
|
Коэффициенты an |
d Uвых, % |
D j, ° |
|
a1 = 1,000 a2 = 0,4999 a3 = 0,1666 a4 = 0,0416 a5 = 0,0083 a6 = 0,0013 a7 = 0,0002 |
0,005 |
0,003 |
|
a1 = 1,000 a2 = 0,4999 a3 = 0,1661 a4 = 0,0416 a5 = 0,0076 a6 = 0,0013 |
0,016 |
0,005 |
|
a1 = 1,000 a2 = 0,4967 a3 = 0,16605 a4 = 0,03705 a5 = 0,00761 |
0,06 |
0,06 |
|
Рис. 6. Зависимости погрешности фазового сдвига Dj (а) и модуля dUвых напряжения выхода (б) |
Анализ полученных результатов показывает, что уже при использовании шести ЦАП можно построить калибратор фазы с высокими метрологическими характеристиками. Погрешность калибратора фазы в основном будет определяться погрешностью настройки ЦАП на заданный масштаб преобразования, паразитными фазовыми сдвигами в ЦАП и сумматорах на высоких частотах, точностью поддержания фазового сдвига 90°.
Экспериментальная проверка макета калибратора фазы показала, что в диапазоне 30 Гц - 20 кГц основная погрешность не превышает 0,1° и достигает максимального значения на верхней частоте указанного диапазона (испытания макета проводили с использованием калибратора фазы, прошедшего метрологическую аттестацию во ВНИИМ).
Литература
1. Федорков Б.Г., Телец В.А., Дегтяренко В.П. Микроэлектронные цифро-аналоговые и аналого-цифровые преобразователи.- М.: Радио и связь, 1984.- 320 с.
2. Гутников В.С. Интегральная электроника в измерительных устройствах. – 2-е изд. – Л.: Энергоатомиздат. 1988. – 304 с.
3. Арутюнов В.С. Электрические измерительные приборы и измерения. Госэнергоиздат, 1958.
4. Сапельников В.М. Нелинейный цифро-аналоговый преобразователь – дискретный аналог синусно-косинусного потенциометра // Измерительная техника. – 1997. - № 1. – С. 32 – 34.
5. Мелик-Шахназаров А.М. Потенциометрический фазовращатель. Радиотехника. Т.12, №5, 1957. - С. 78-79.
6. Сапельников В. М. ЦАП в калибраторах фазы / Изд-е Башкирск. ун-та. - Уфа, 1997. - 152 с.
7. Сапельников В.М., Кравченко С.А., Чмых М.К. Проблемы воспроизведения смещаемых во времени электрических сигналов и их метрологическое обеспечение / Изд-е Башкирск. гос. ун-та. – Уфа, 2000. – 196 с.
8. Электроника: Справочная книга / Под ред. Ю.А. Быстрова. - СПб.: Энергоатомиздат, 1996. - 544 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
