Функциональные цифро-аналоговые преобразователи и их роль в развитии приборостроения, страница 3

Моделирование  многочлена осуществляется каскадно соединенными ЦАП (рис. 4) [6, 7].

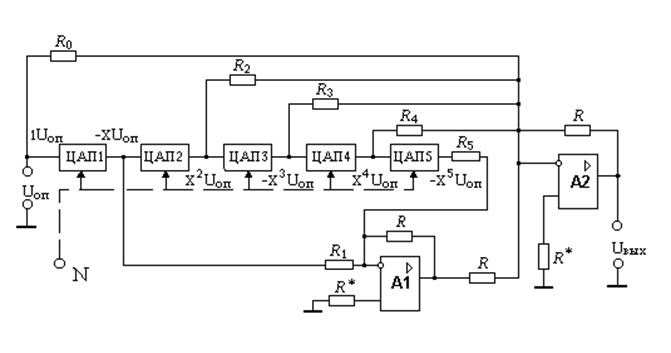
Рис. 4. Схема функционального цифро-аналогового преобразователя

В качестве ЦАП, изображенных на схеме, применяют умножающие ЦАП, которые могут работать с двухполярным опорным напряжением. Выходное напряжение таких ЦАП определяется по формуле:

,

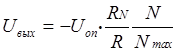где N - текущий цифровой код, который изменяется в пределах от 0 до N_max-1; N_max=2^m, m - разрядность ЦАП; R - сопротивление матрицы резисторов; R_N - сопротивление резистора в цепи обратной связи ОУ ЦАП; U_оп - опорное напряжение. Отношение 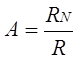 называют масштабным коэффициентом или масштабным множителем. Его можно изменять в широких пределах, изменяя R_N.

В схеме, приведенной на рис. 4, при подаче на цифровые входы ЦАП кода N, на выходе 1-го ЦАП формируется напряжение, равное:

U₁=-U_опA.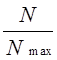

Это напряжение является входным для 2-го ЦАП, а напряжение на его выходе будет определяться соотношением:

U₂=-U₁A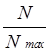=U_оп(- А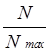)².

Продолжая этот ряд, для k-го ЦАП можно записать:

U_k= U_оп(- А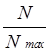)^k.

Напряжения с выходов ЦАП через резисторы R₁, R₂, ..., R₅ подаются на вход сумматора А2. Для обеспечения необходимого знака, напряжения с выходов первого и пятого ЦАП проходят через инвертор А1. Дополнительно на сумматор через резистор R₀подается опорное напряжение. На выходе сумматора формируется напряжение U_вых:

U_вых=- ();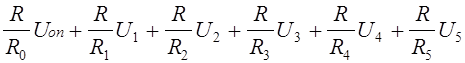

 или, с учетом предыдущего уравнения:

U_вых=- U_оп.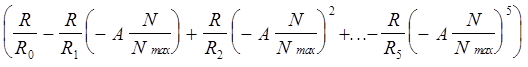

Если обозначить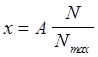, , 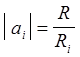то последнее уравнение примет вид:

U_вых=- U_оп(a₀+a₁x+a₂x²+а₃х³+а₄х⁴+a₅x⁵)»- U_опf(x).

Коэффициенты многочлена, реализуемого данной схемой, имеют следующие знаки: а₀>0, а₁>0, а₂>0, а₃<0, а₄>0, а₅>0. Если коэффициенты имеют другие знаки, то схема претерпевает лишь незначительные изменения. Таким образом, мы получаем выходное напряжение пропорциональное аппроксимируемой функции f(x).

Необходимо указать на ограничение, которое накладывается каскадным включением ЦАП на диапазон изменения масштабного коэффициента А. При подаче на цепочку ЦАП кода, близкого к N_max, выходное напряжение k-го ЦАП пропорционально U_оп(- A)^k. Для А>1 эта величина возрастает по геометрической прогрессии и может приводить к насыщению операционных усилителей. Поэтому выгодно устанавливать А равным 1 и аппроксимировать функцию исходя из того, что аргумент х изменяется от 0 до 1.

Из вышесказанного следует, что для воспроизведения многочлена P_n(x) степени n необходимо n каскадно включенных ЦАП. Коэффициенты многочлена реализуются подбором резисторов R, R₀ ,R₁, ... R_k, а знаки слагаемых устанавливаются при помощи инвертора.

Для того чтобы погрешность, вызванная аппроксимацией (методическая погрешность), была минимальна, необходимо соответствующим образом подобрать коэффициенты многочлена.

Нами рассмотрены три метода вычисления этих коэффициентов.

Наиболее распространенный метод аппроксимации функции f(x)– ее разложение в ряд Тейлора. В общем виде это разложение функции f(x)в окрестности точки х₀ осуществляется по формуле:

 .

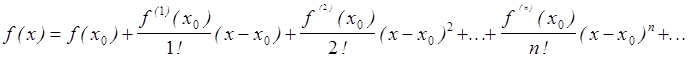Разложение функции в ряд Тейлора не является единственным. Существует возможность разложить функцию в ряд по обобщенным многочленам, например, по многочленам Лежандра, Чебышева, Якоби, Эрмита или Лагерра. Здесь мы остановимся на многочленах Чебышева, поскольку они дают наилучшее приближение.

Для нахождения коэффициентов C_k разложения по многочленам Чебышева 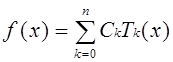 используем следующие формулы:

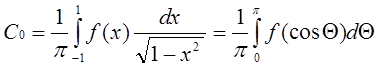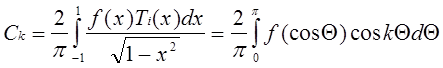, ,  k  > 0.

Подставляя вместо степеней х их выражения через многочлены Чебышева, а затем, приводя подобные члены при многочленах одной степени, получим искомый многочлен P_n(x)= .

Оценить погрешность, даваемую разложением функции f(x) в ряд по многочленам Чебышева в общем виде, очень трудно. Но согласно общим теоремам теории аппроксимации это разложение дает наилучшее приближение из всех возможных. Необходимо также отметить, что разложение функции f(x)по многочленам Чебышева возможно только для функций, имеющих непрерывную первую производную на отрезке [-1, 1]. Это условие обеспечивает сходимость ряда к функции f(x). Для всех простейших функций это условие выполняется.