Функциональные цифро-аналоговые преобразователи и их роль в развитии приборостроения, страница 4

Следующий метод основан на теории интерполяции. В этом случае строят многочлен, который в n+1 заданных точках х₀, х₁, ... x_n, принимает значения f(x₀), f(x₁), . . . f(x_n), а в остальных точкахотрезка [a,b], принадлежащего области определения f(x), приближенно представляет функцию f(x)с той или иной степенью точности. Для нахождения коэффициентов многочлена a_k составляется система уравнений:

,     ( i = 0, 1, 2,  . . . , n ),

которая легко решается, например, методом Крамера.

Пример.

Калибратор фазы с линейным преобразованием

управляющего кода в фазовый сдвиг

Широкое распространение получают калибраторы фазы, принцип действия которых заключается в суммировании двух синусоидальных напряжений, сдвинутых одно относительно другого на 90°. Диапазон регулирования фазового сдвига при этом составляет 0-90°, а его расширение до 360° осуществляется введением коммутатора опорных напряжений.

При регулировании фазового сдвига в пределах 0-90° выходное напряжение калибратора фазы формируется в соответствии с зависимостью

,                         (*)     

где U_вх - амплитуда опорных напряжений;

k₁ и k₂ - весовые коэффициенты.

Амплитуда и фаза выходного напряжения связаны с весовыми коэффициентами k₁ и k₂ соотношениями

;                                           

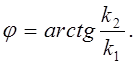
Калибраторы фазы, управляемые цифровым кодом, должны обеспечивать линейное преобразование управляющего кода в фазовый сдвиг выходного напряжения. Кроме того, в большинстве практических случаев необходимо обеспечить постоянство амплитуды выходного напряжения во всем диапазоне регулирования фазового сдвига. Для выполнения этих требований весовые коэффициенты k₁ и k₂ должны быть связаны с управляющим кодом нелинейными зависимостями.

В калибраторе фазы, структурная схема которого представлена на рис.5., выходное напряжение является суммой двух синусоидальных напряжений и , сдвинутых одно относительно другого на 90°. Они формируются из входного синусоидального напряжения  цепью каскадно включенных цифроаналоговых преобразователей ЦАП1 - ЦАП7 и инвертирующими сумматорами А1 - А4.

Передаточная функция i-го ЦАП  выражается линейной зависимостью

,

где b_i - масштаб преобразования i-го ЦАП;

N и N_max - текущее и максимальное значения управляющего кода.

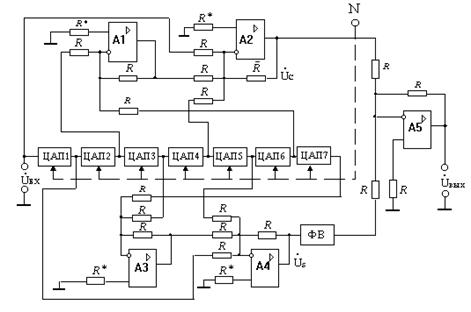
Рис. 5. Калибратор фазы с линейным преобразованием управляющего

кода в фазовый сдвиг

Применяемые в калибраторе фазы ЦАП имеют малое выходное сопротивление, что допускает их каскадное включение без нарушения нормального режима работы каждого отдельно взятого ЦАП. Поэтому передаточную функцию n каскадно включенных ЦАП с достаточной степенью точности можно записать в виде

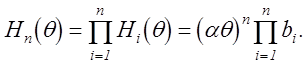
На вход первого ЦАП, являющегося входом калибратора фазы, с внешнего генератора поступает синусоидальное напряжение . Из него цепью каскадно включенных ЦАП формируются напряжения, амплитуды U_n которых связаны с управляющим кодом соотношением

где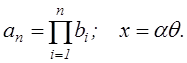

Напряжения  с выходов ЦАП и входное напряжение используются для формирования двух синфазных напряжений  и , причем напряжение  формируется из входного напряжения и напряжений с выходов ЦАП с четными номерами, а выходные напряжения нечетных ЦАП используются для формирования напряжения . Полагая весовые коэффициенты суммируемых напряжений  и  равными единице и учитывая дополнительное инвертирование соответствующих напряжений сумматорами А1 и А3,зависимости амплитуды напряжений  и  от управляющего кода в соответствии с (4.5) можно представить в виде

U_s =- U_вх(a₁x- a₃x³+a₅x⁵- a₇x⁷) = U_вхk₂;

U_c =- U_вх(1- a₂x²+a₄x⁴- a₆x⁶) = U_вхk₁.

Таким образом, амплитуды напряжений  и  связаны с амплитудой синусоидального напряжения , поступающего на вход калибратора фазы, коэффициентами k₁ и k₂, которые в свою очередь имеют нелинейную зависимость от управляющего кода.

k₁ = 1- a₂x²+a₄x⁴- a₆x⁶;

k₂ = a₁x- a₃x³+a₅x⁵- a₇x⁷.