Функциональные цифро-аналоговые преобразователи и их роль в развитии приборостроения
Сапельников В.М.
Башкирский государственный университет, 450074, г. Уфа, ул. Фрунзе,32, тел. (3472)23-65-74,факс. (3472)23-66-80 VSapelnikov@bsu.bashedu.ru
Цифро-аналоговые преобразователи (ЦАП) широко применяются для преобразования сигналов в информационно-измерительной технике, радиотехнике и приборостроении. Они являются мощным средством увеличения точности отсчета. Однако существующие ЦАП могут выполнять только линейное преобразование вида Uвых=kUоп. В то же время в различных областях техники необходимо с высокой точностью воспроизводить нелинейные функциональные зависимости. Например, такая необходимость возникает при построении цифроуправляемых фазовращателей и калибраторов фазы, так как зависимость фазового сдвига от изменения регулируемой величины всегда нелинейна. Наиболее предпочтительный способ для осуществления этой операции – использование ЦАП.
Для воспроизведения нелинейных функциональных зависимостей и моделирования их с помощью линейных ЦАП мы использовали два вида аппроксимации: кусочно-линейную аппроксимацию и аппроксимацию степенными рядами. Каждый из упомянутых видов аппроксимации предполагает свой способ аппаратной реализации. Однако оба способа для увеличения дискретности воспроизводимой функции используют стандартные многоразрядные ЦАП.
Рассмотрим первый способ, в котором используется линейная аппроксимация воспроизводимой функциональной зависимости y= f(x) в интервале [a+i(b-a)/n,a+(i+1)(b-a)/n]. Здесь [a, b] - отрезок, который разбивается на интервалы, (b-a)/n – величина интервала аппроксимации функциональной зависимости f(x), i=0, 1, 2, ..., n-1 (i - номер интервала аппроксимации, n - число отрезков аппроксимации зависимости f(x)). Полагаем, что на отрезке аппроксимации функция неотрицательна, хотя данный способ может быть расширен и на отрицательные значения функции.
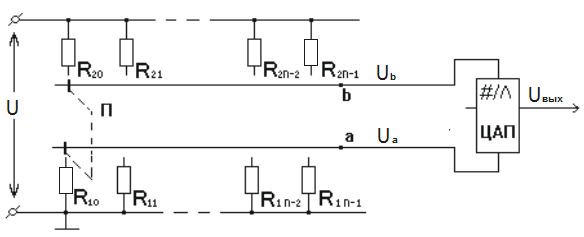 |
Рис.1. Функциональный цифро-аналоговый преобразователь
На рис.1 приведена схема, иллюстрирующая использование линей ной аппроксимации для воспроизведения функциональной зависимости f(x). Значения сопротивлений R1i, R2i, R0 связаны между собой соотношениями:
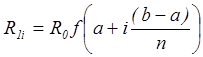 ,
, 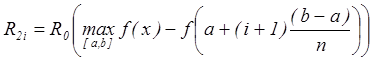 .
.
Напряжения в схеме рис. 1 будут распределяться следующим образом:
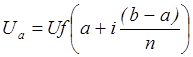 ,
, 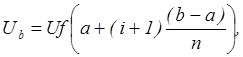
где U- напряжение, подводимое к нелинейному ЦАП.
С помощью линейного ЦАП
выходное напряжение Uвых изменяется от величины 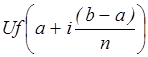 до
до 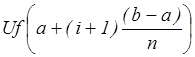 ,
приближенно воспроизводя в i-ом интервале зависимость f(x) c заданным шагом квантования. Для изменения интервала
регулирования функциональной зависимости f(x) (старший разряд нелинейного ЦАП)
используется ключ П (рис. 1).
,
приближенно воспроизводя в i-ом интервале зависимость f(x) c заданным шагом квантования. Для изменения интервала
регулирования функциональной зависимости f(x) (старший разряд нелинейного ЦАП)
используется ключ П (рис. 1).
Естественно, что при
таком построении функционального ЦАП последний имеет методическую погрешность,
вызванную линейной аппроксимацией функциональной зависимости f(x) в интервале [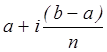 ,
,
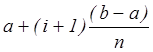 ]. Эта погрешность определяется выражением
]. Эта погрешность определяется выражением
![]() ,
,
где y1i - уравнение
прямой, аппроксимирующей зависимость f(x) в интервале [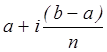 ,
,
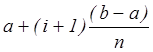 ]. Введем обозначение
]. Введем обозначение 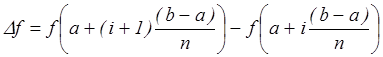 , тогда уравнение прямой запишется в виде:
, тогда уравнение прямой запишется в виде:
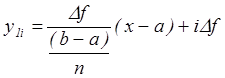 .
.
Здесь 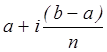 £ x £
£ x £ 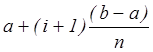 . Методическая погрешность воспроизведения
функции f(x)
будет зависеть в
первую очередь от ее вида и выбранного отрезка аппроксимации, а также от номера
и количества участков аппроксимации.
. Методическая погрешность воспроизведения
функции f(x)
будет зависеть в
первую очередь от ее вида и выбранного отрезка аппроксимации, а также от номера
и количества участков аппроксимации.
Нелинейные ЦАП, аппроксимирующие функции sinj и cosj, широко применяются при построении калибраторов фазы и фазовращателей (синусно-косинусные потенциометрические фазовращатели), в которых для формирования напряжения выхода реализуется соотношение:
![]() .
.
Пример.
В качестве примера рассмотрим построение функционального цифроаналогового преобразователя – дискретного аналога синусно-косинусного потенциометра [4].
Известные синусно-косинусные потенциометры нашли применение в радиотехнике, информационно-измерительной технике [5]. Они используют профилированную намотку провода и имеют скользящий контакт, что нетехнологично, не позволяет получить хорошие метрологические характеристики и не дает возможность применить их в микроэлектронике.
Выполнение синусно-косинусного потенциометра из набора резисторов и ключей привело бы к необходимости применения большого количества резисторов разных номиналов и ключей. Так, для дискретного потенциометра, воспроизводящего синусную зависимость сопротивления от изменения входного кода в диапазоне от 0 до 90° и дискретностью 0.1°, потребовалось бы 900 резисторов и 901 ключ.
Вполне очевидно, что подобные дискретные синусные потенциометры очень громоздки и, кроме того, при такой реализации синусного потенциометра невозможно производить поразрядное регулирование воспроизводимой функциональной зависимости.
От этих недостатков свободна схема, приведенная на рис. 2, построенная на базе нелинейного ЦАП — цифро-аналогового преобразователя, воспроизводящего нелинейную зависимость sinj.
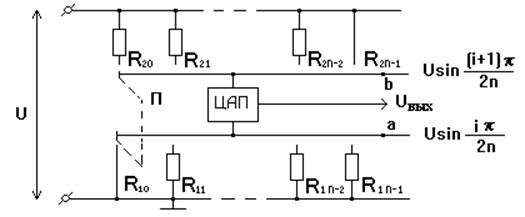
Рис. 2. Функциональный ЦАП - дискретный аналог синусного потенциометра
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.