Функциональные цифро-аналоговые преобразователи и их роль в развитии приборостроения, страница 2

С помощью сдвоенного ключа линейный многоразрядный ЦАП, подключается к резисторам R_1i и R_2i - и образует преобразователь, моделирующий зависимость sinj в интервале от ip/2n до (i+1)p/2n. Здесь p/2n - интервал аппроксимации функциональной зависимости sinj,   i=0,1,2,...,n-1 (i-номер интервала аппроксимации, n-число отрезков аппроксимации зависимости sinj  в интервале от 0 до p/2 ). В качестве многоразрядного линейного ЦАП можно использовать любой ЦАП с постоянным входным сопротивлением R₀.

Значения сопротивлений R_1i, R_2i, R₀ определяются из соотношений:

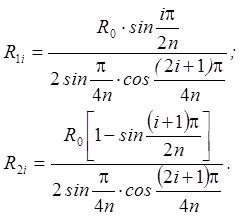
Напряжения в схеме рис. 2 будут распределяться следующим образом:

,                                       

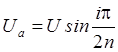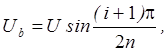
 где U- напряжение, подводимое к дискретному аналогу синусного потенциометра – функциональному ЦАП.

С помощью линейного ЦАП выходное напряжение Uвых изменяется от величины  до 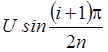, приближенно воспроизводя в i-ом интервале зависимость sinj необходимым числом разрядов. Для изменения интервала регулирования функциональной зависимости sinj (старший разряд нелинейного ЦАП) используется ключ П (рис.2).

Естественно, что при таком построении дискретного аналога синусного потенциометра последний имеет методическую погрешность, вызванную линейной аппроксимацией зависимости sinj в интервале [ip/2n, (i+1)p/2n]. Эта погрешность определяется выражением

,

где y_1i - уравнение прямой , аппроксимирующей зависимость sinj в интервале [ip/2n, (i+1)p/2n]:

.              

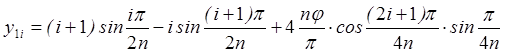 Здесь ip/2n £j£ (i+1)p/2n.

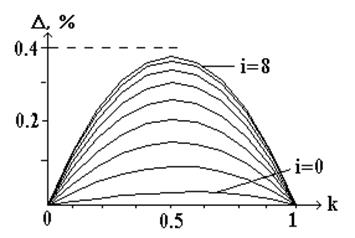
Рис. 3. Распределение методической погрешности дискретного аналога синусного потенциометра внутри интервалов аппроксимации (n=9).

На рис. 3 приведена зависимость методической погрешности воспроизведения зависимости sinj внутри интервала аппроксимации (D) для n=9. В этом случае старший разряд регулирования фазового сдвига составляет 10° . Для удобства введена новая переменная k из соотношения

j = (i+k)×p/2n.   Здесь 0 £ k £ 1.

Наибольший интерес представляет максимальная погрешность, получаемая при аппроксимации последнего интервала зависимости sinj. В табл. 1 приведены максимальные величины погрешности в зависимости от числа интервалов аппроксимации.

Таблица 1

Так, в случае n=9, она составляет величину менее 0,4 %, что может быть приемлемо для многих практических применений.

В случае одновременного использования синусного и косинусного преобразователей, как это сделано в работе [6] для построения фазовращателя, методическая погрешность воспроизведения фазового сдвига получается небольшой, поскольку погрешности преобразователей имеют один знак. Так, при подекадном регулировании фазового сдвига (n=9) методическая погрешность, вызванная аппроксимацией зависимостей sinj и cosj , составляет всего полминуты.

Дискретный аналог синусного потенциометра (рис.2) дает возможность изменять зависимость sinj в пределах одного квадранта. Все эти же элементы используются и для регулирования зависимости sinj во всех четырех квадрантах, но в третьем и четвертом квадрантах для получения отрицательных величин используется инвертор или  во входной цепи (инвертируется входное напряжение), или в выходной цепи (инвертируется выходное напряжение). Кроме того, все элементы схемы рис.2 применяются и для построения дискретного аналога косинусного потенциометра, поскольку cosj=sin(p/2+j). Таким образом, схема, приведенная на рис. 2, может почти полностью обеспечить  одновременное моделирование и синусного, и косинусного преобразователей.

          Кроме того, рассмотренный способ применим для построения цифроуправляемых потенциометрических и мостовых фазовращателей.

Второй способ, использующий степенную аппроксимацию, заключается в следующем. На рассматриваемом отрезке [a, b] функция f(x) заменяется многочленом

P_n(x)=.