Расчет системы автоматического управления электроприводом при номинальном напряжении двигателя: Uн = 220 В и перерегулировании скорости: σ = 25 %, страница 4

и ЛАХ корректирующего устройства представлены на листе №2.  Для обеспечения более простой схемы реализации КУ желаемая ЛАХ при частоте сопряжения 100рад/с имеет наклон -20Дб/дек.  При пересечении Желаемой ЛАХ с ЛАХ нескорректированной системы, она совпадает с ней. (имеет наклон -60Дб/дек).

Передаточная функция желаемой ЛАХ:

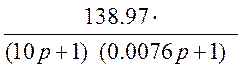
 Т₁=10с, Т₂=0,0076с;

3.3.1 Схемная реализация КУ при параллельной коррекции САУ.

ЛАХ корректирующего устройства на высоких частотах имеет при Т₂=0,0076с излом +60ДБ/дек, данный излом не может сильно повлиять на устойчивость САУ и на переходный процесс в целом, поэтому будем считать, что ЛАХ корректирующего устройства прямая имеющая наклон +20Дб/дек.

Имеем форсирующее звено 1-го порядка, передаточная функция КУ:

  Т₁=10с,

       

       

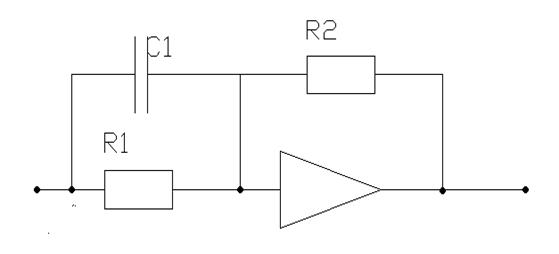
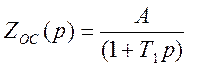
В результате расчётов получаем параметры элементов цепи корректирующего устройства:

                                                        

.

3.4 Определение фактических запасов устойчивости
скорректированных систем

1. Последовательная коррекция.

Строим диаграмму Боде скорректированной системы с последовательным корректирующим устройством.

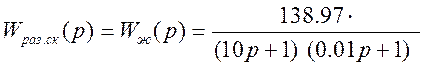
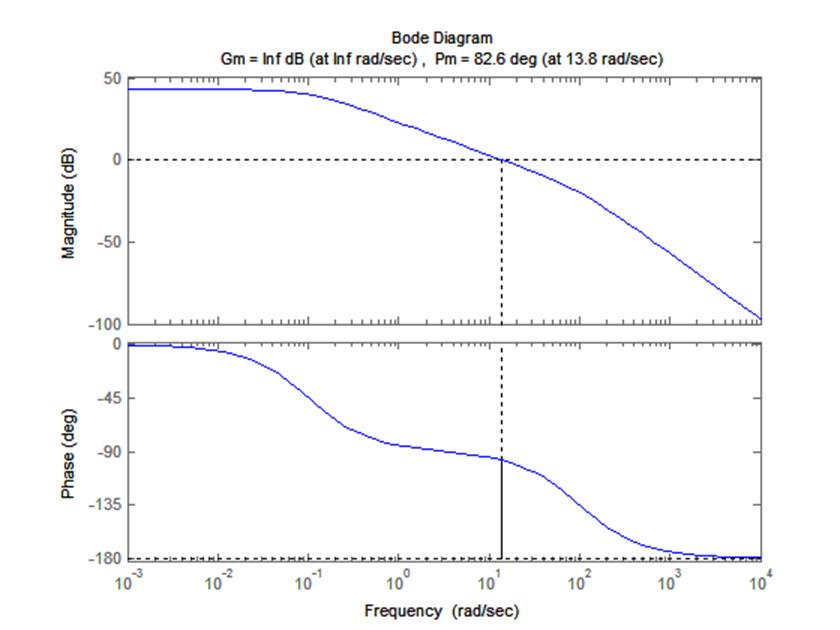
По данной диаграмме видно, что система устойчива (в области частот до пересечения ЛАХ значения нуля ЛФХ не пересекает значение –180º). Реальные запасы устойчивости системы:

– по фазе: 82.6º;

– по амплитуде: бесконечность.

2. Параллельная коррекция

Строим диаграмму Боде скорректированной системы с параллельным корректирующим устройством.

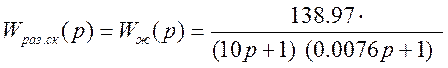
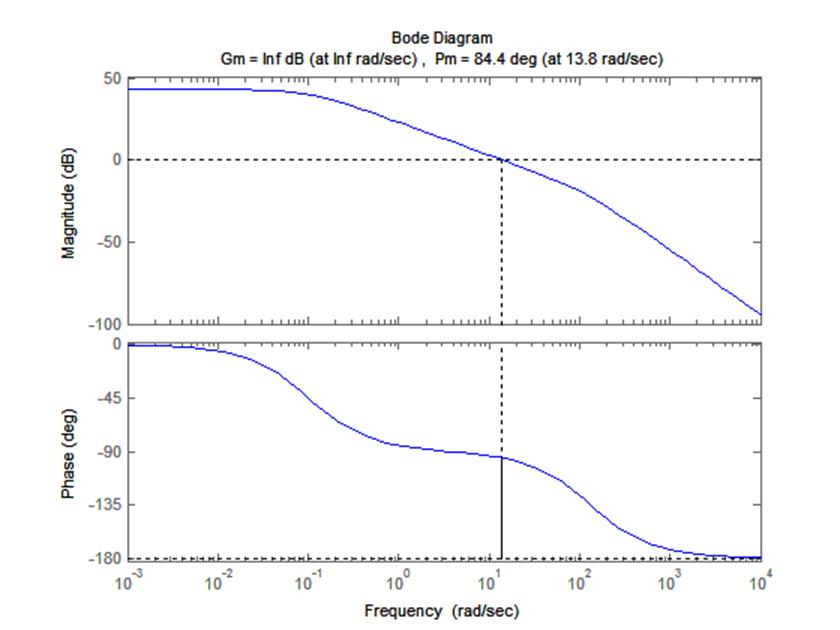
По данной диаграмме видно, что система устойчива (в области частот до пересечения ЛАХ значения нуля ЛФХ не пересекает значение –180º). Реальные запасы устойчивости системы:

– по фазе: 84.4º;

– по амплитуде: бесконечность.

4. Структурно параметрический синтез регуляторов.

                При последовательной коррекции САУ наибольшее распространение получил принцип синтеза регуляторов контуров систем, построенных по схеме подчинённого управления. Основными критериями настройки стали модульный оптимум и симметричный оптимум.

Основной задачей синтеза контура считается определение структуры и параметров последовательного корректирующего устройства (регулятора). При настройки на модульный оптимум ставится требование, чтобы передаточная функция разомкнутой скорректированной системы имела вид: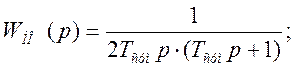                                

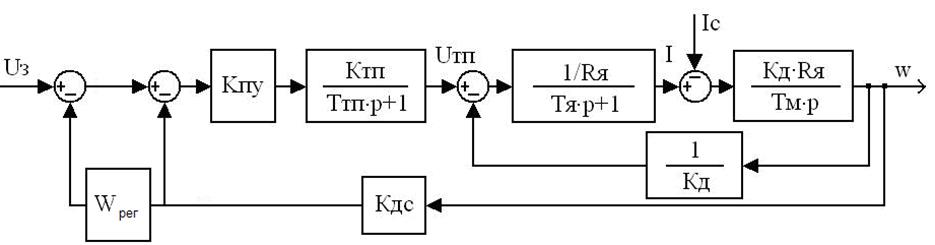
Рис.4Структурная схема САУ:

Передаточная функция объекта определяется:

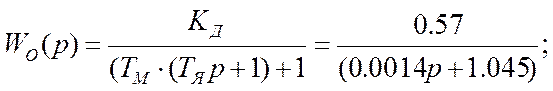  (8.2)

Передаточная функция устройства обратной связи определяется:

Передаточная функция неизменяемой части выразится как

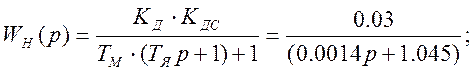 где Tсум=0.0014с;

При настройки на модульный оптимум получим соответственно передаточную функцию разомкнутой скорректированной системы Wмо(p) и регулятора Wрег(p):

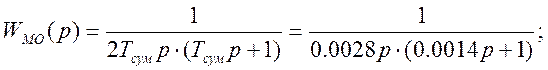
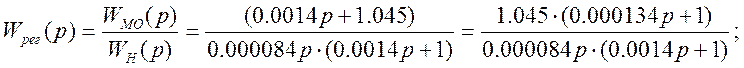 (8.3)

Корректирующее устройство представляет собой ПИ – регулятор с коэффициентом K=1.045, и постоянной времени Tрег=0.0014c;

Стандартная передаточная функция замкнутого оптимизированного контура имеет вид:

Kос=;

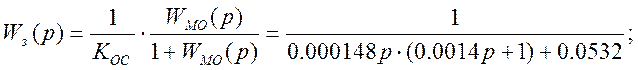           (8.4)

В действительности передаточные функции замкнутого контура определится:

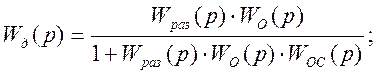                                             (8.5)

Передаточная функция разомкнутой системы определится:

                                              

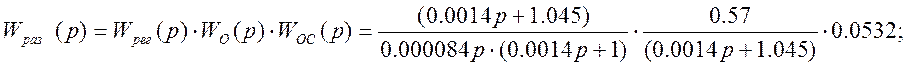
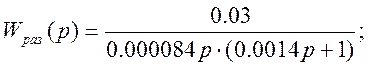
Отсюда действительная передаточная функция замкнутой системы определится:

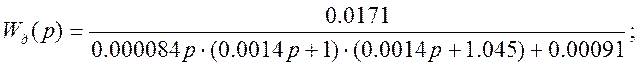                  (8.7)

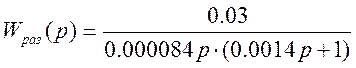
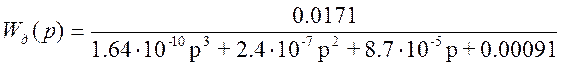
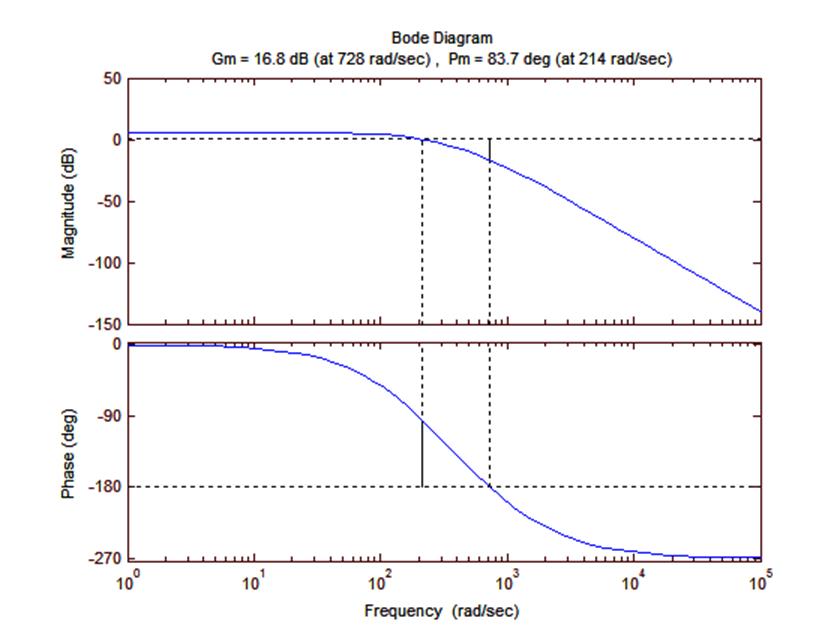
Рис 4.1. Диаграмма Боде для САУ настроенной на модульный оптимум.

По данной диаграмме видно, что система устойчива (в области частот до пересечения ЛАХ значения нуля ЛФХ не пересекает значение –180º). Реальные запасы устойчивости системы:

– по фазе: 83.7º;

– по амплитуде: 16.8.

4.1. Схемная реализация регулятора.

 

              

    

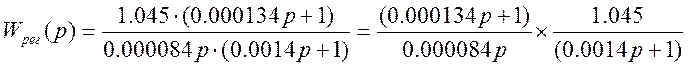
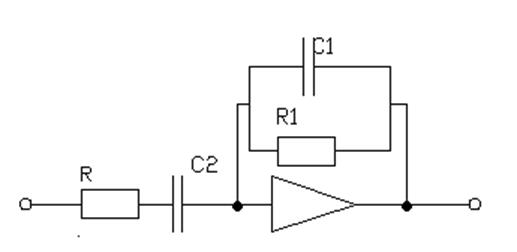
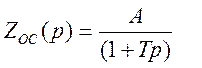
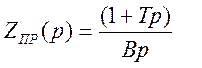
В результате расчётов получаем параметры элементов цепи корректирующего устройства:

Ом      МкФ

Ф  Ом

5.Построение переходных процессов скорректированной системы при единичном входном воздействии.

Постоим переходные процессы для скорректированных систем и в совокупности с найденными схемными реализациями и определим наиболее качественный тип коррекции для исходной САУ.

1.Переходный процесс для САУ с последовательной коррекцией:

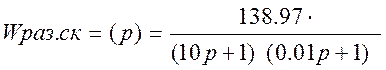
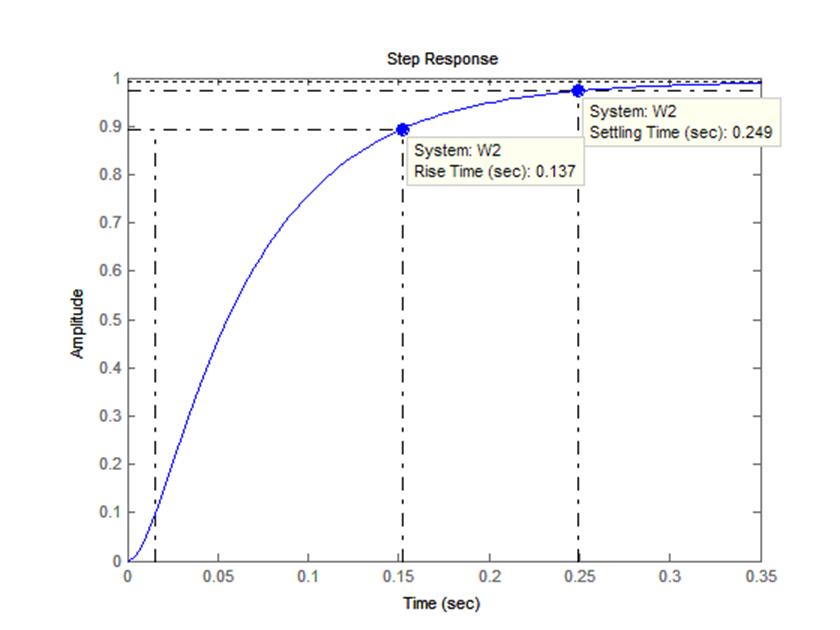
Время переходного процесса:

 0.249с;

Время первого согласования:

 0.137с;

Перерегулирование:

 отсутствует.

2.Переходный процесс для САУ с параллельной коррекцией:

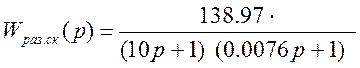
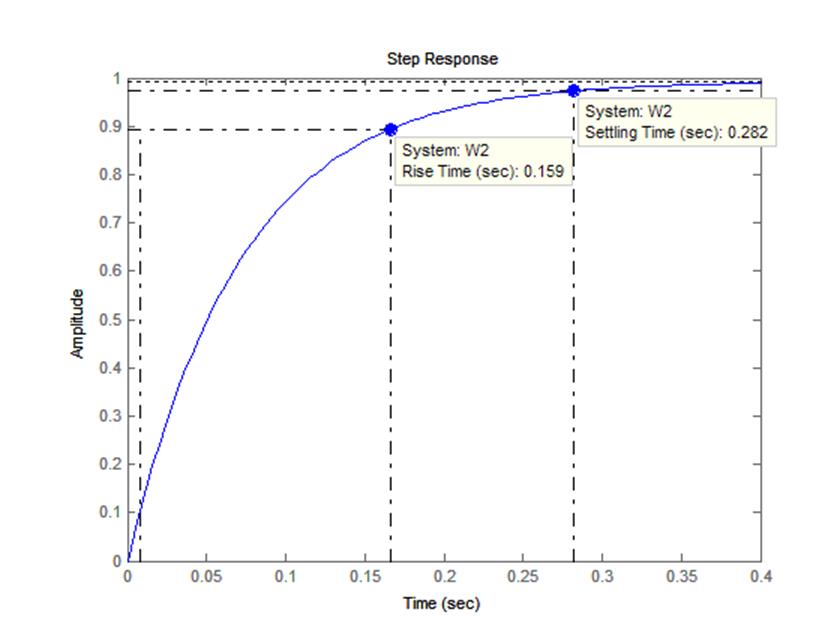
Время переходного процесса:

0.282с;

Время первого согласования:

0.159с;

Перерегулирование:

отсутствует.

3.Переходный процесс для САУ настроенной на модульный оптимум.

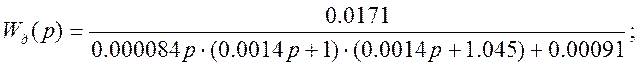
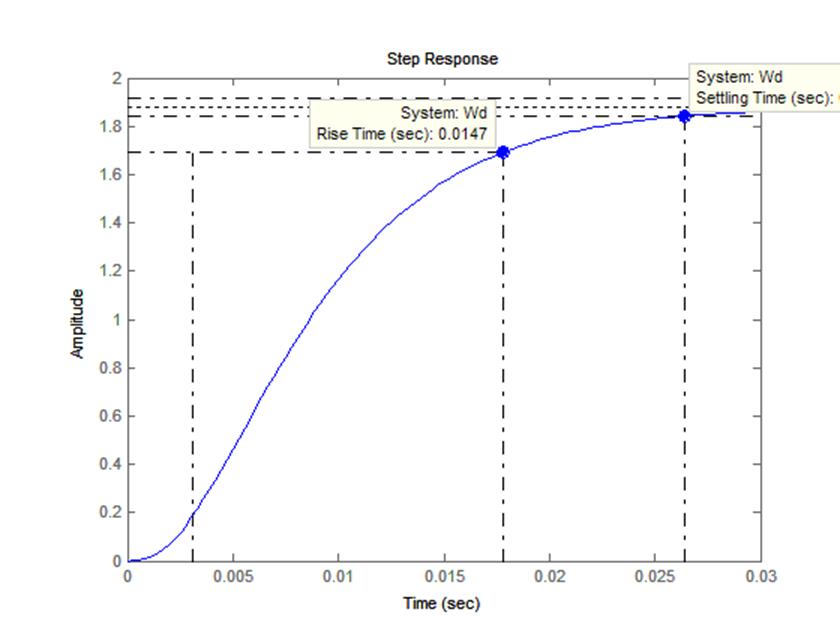
Время переходного процесса:

t=0.0264c;

Время первого согласования:

t=0.0147c

Перерегулирование отсутствует.