Расчет системы автоматического управления электроприводом при номинальном напряжении двигателя: Uн = 220 В и перерегулировании скорости: σ = 25 %, страница 2

ПФ системы по управляющему воздействию

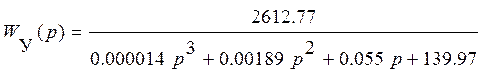
Характеристический полином:

Для того чтоб САУ была устойчива необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак.

Таблица 2.1. – Таблица Рауса

Из данной таблицы можно сделать вывод о том что САУ не устойчива

 (в первом столбце при  a₀>0 имеется отрицательный элемент в 3-ей строке).

2.2 Анализ устойчивости  САУ с использованием
частотного критерия

В качестве частотного критерия устойчивости задан критерий Найквиста.

Для анализа САУ необходимо использовать передаточную функцию системы по управляющему воздействию в разомкнутом состоянии.

ПФ системы по управляющему воздействию (разомкнутая)

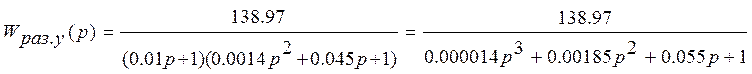
Все «нули» данной передаточной функции отрицательны, следовательно  САУ в разомкнутом состоянии устойчива.

Для того чтоб замкнутая система была устойчива необходимо и достаточно чтоб амплитудно-фазовая характеристика  разомкнутой системы не охватывала точку (-1, j0)

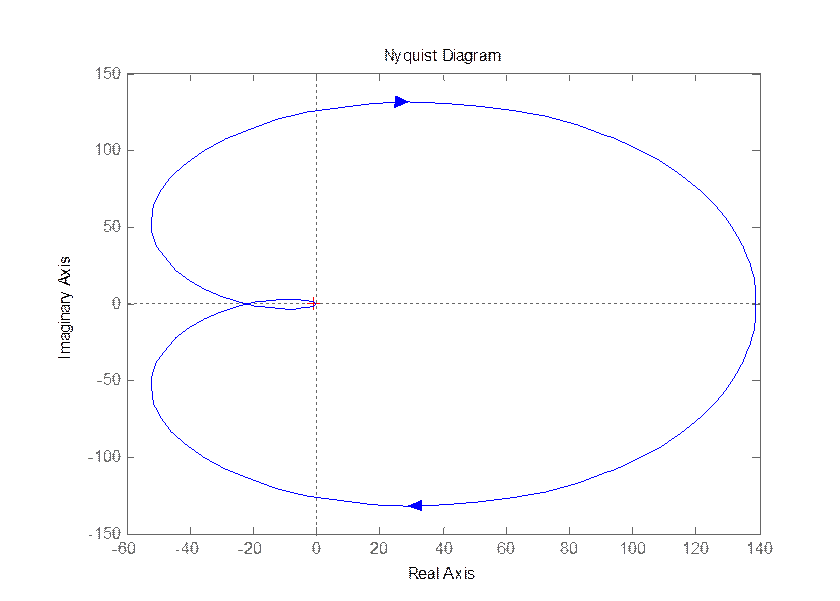
Рис 2.2

Годограф Найквиста.

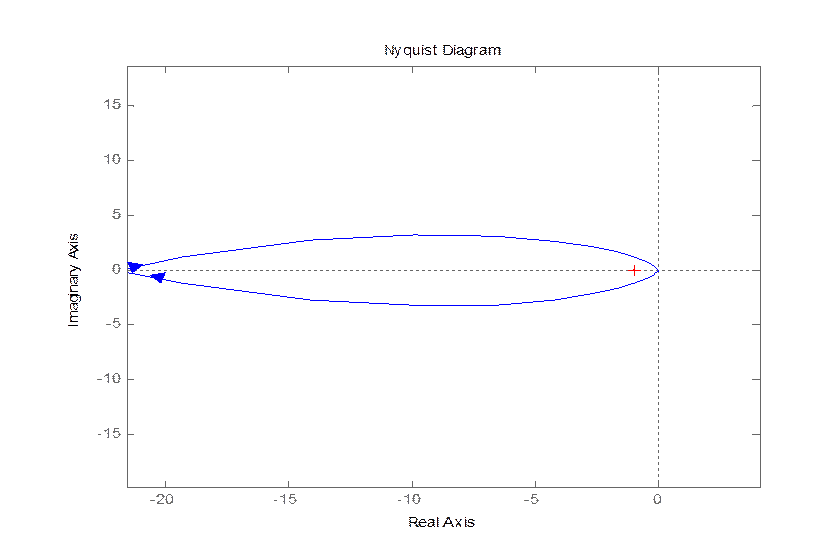
Рис 2.3

Годограф Найквиста (Увеличенный)

Годограф охватывает точку (-1, j0), Система не устойчива.

2.3 Анализ влияния коэффициента усиления
разомкнутой САУ на устойчивость

          По корневому годографу определим критический коэффициент усиления САУ, при котором она будет находиться на границе устойчивости.

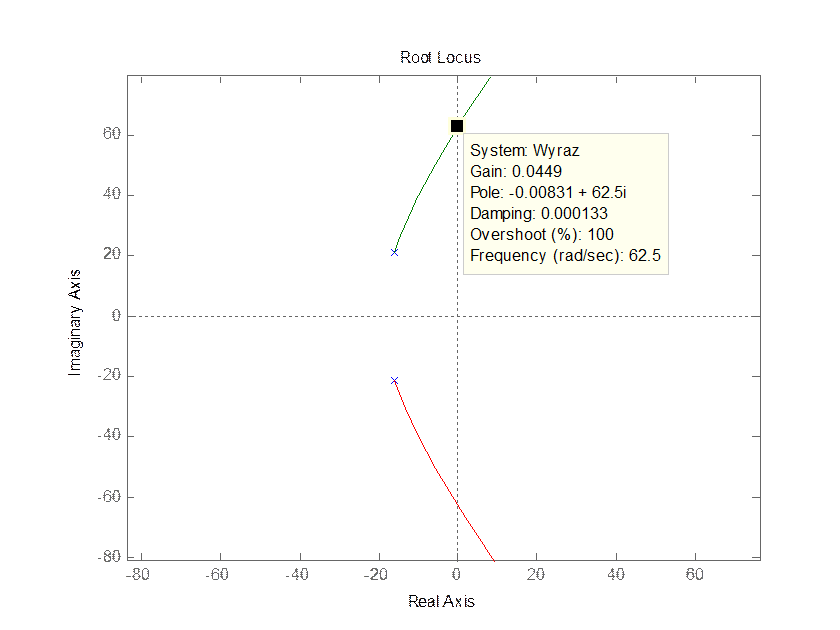
        Рис 2.4

Корневой годограф.

Критическое значение коэффициента усиления системы находиться в точке пересечении ветвей годографа и оси ординат. Вправо от оси ординат лежат значения коэффициента усиления системы, при которых система будет неустойчивой, а слева от оси лежат значения, при которых система будет устойчива.

          Найдем критическое значение коэффициента усиления разомкнутой системы:

К_КР1 = К_тр*0.0449 = 139*0.0449=6.24

          При К > К_КР система будет неустойчивой. При найденном значении коэффициента передачи разомкнутой системы, () система будет неустойчива. Для того чтоб система была устойчивой необходимо выполнить коррекцию САУ.

2.4 Построение и анализ диаграммы Боде
для разомкнутой САУ

Диаграмма Боде поможет оценить устойчивость САУ, а также позволит ещё раз оценить критический коэффициент усиления разомкнутой САУ .

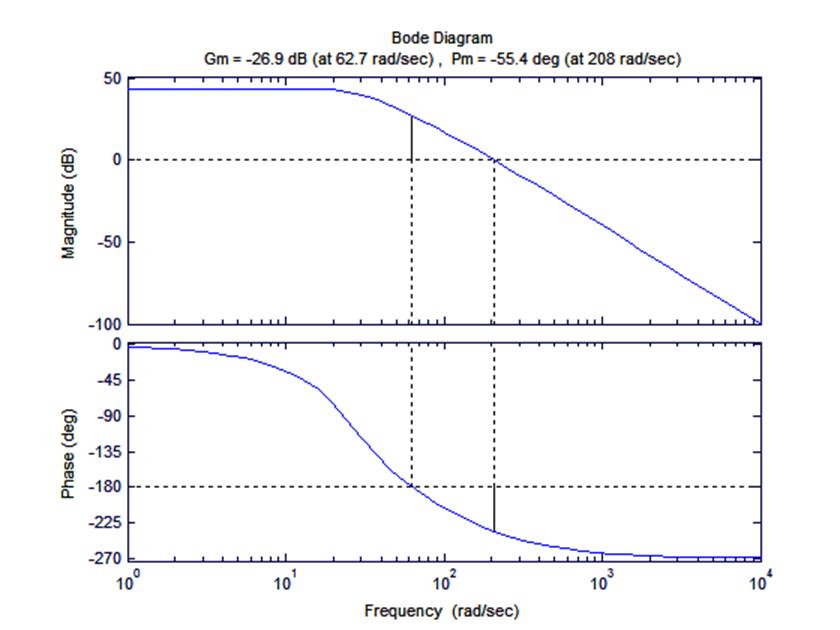
Рис 2.5

Диаграмма Боде для разомкнутой САУ.

Система является не устойчивой, так как в области частоты среза ЛФЧХ превышает значение фазы (-180)⁰

          По ЛАХ определяем критический коэффициент передачи разомкнутой системы: (20lgK=26.9).

 

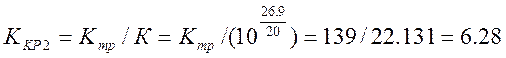
          Найденный коэффициент больше того что был найден с помощью корневого годографа, т.е. K_KP2=6.28 включает в себя значение K_KP1=6.24 следовательно система устойчива при K_KP=6.28.

Определим частоту среза для данной САУ:

 рад/с

Фаза при частоте среза -235.4⁰

Отрицательные запасы устойчивости по фазе(-26.9) и по модулю(55.4) отражены на рис 2.5

          По виду ЛАХ можно определить:

1)  Разомкнутая САУ статическая (первоначальный наклон характеристики равен нулю);

2)  наклон характеристики в зоне частоты среза: -26.9/((208-62.7) =  -18.5 дБ/дек (так как данный наклон одинаков для ЛАХ в зоне 1 декады от частоты среза, то система не будет иметь колебательности);

2.5 Выводы по анализу устойчивости САУ

          Система является неустойчивой. Для обеспечения устойчивости требуется снизить коэффициент передачи разомкнутой системы (тогда она не будет удовлетворять заданным требованиям устойчивости) или ввести корректирующие звенья.

3. Синтез САУ.

Для синтеза корректирующего устройства используем методы последовательной и параллельной коррекции. В итоге будет выбрана та САУ, корректирующее устройство которой будет наиболее простой в схемной реализации. Также устройство должно обеспечивать запас устойчивости по модулю и фазе.

3.1  Расчёт и построение асимптотической ЛАХ
исходной САУ и желаемой ЛАХ.

3.1.1 Исходная ЛАХ.

Передаточная функция разомкнутой системы по управляющему воздействию:

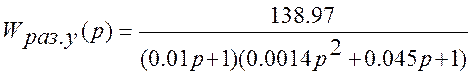
Система состоит из трех звеньев: усилительного, апериодического и звена второго порядка.

Постоянные времени системы:

с; с.

          По данной передаточной функции рассчитываем положение асимптотических участков: