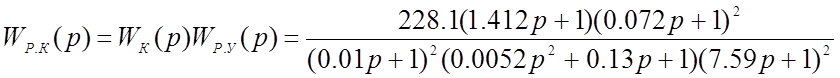
Диаграмма Боде для данной системы изображена на рис. 3.6.1.
по фазе: 81.9º, по амплитуде: 30.5 дБ.
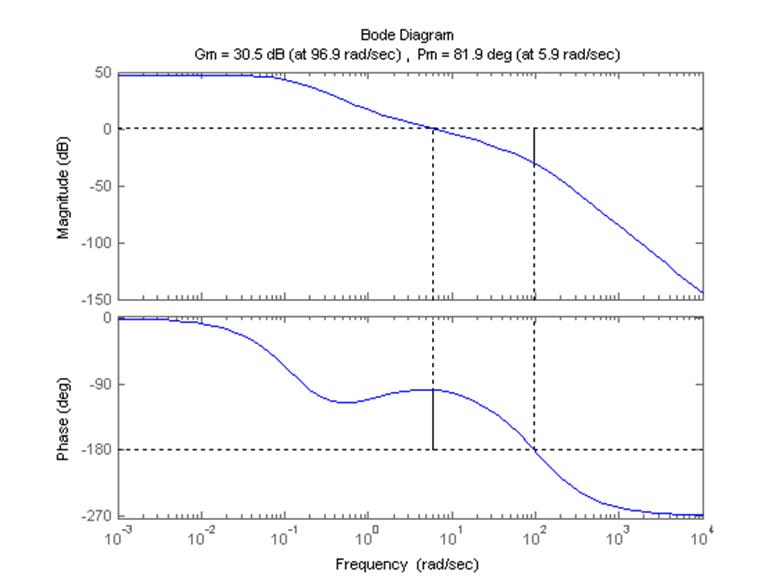
Рисунок 3.6.1 – ЛФЧХ разомкнутой скорректированной системы.
3.6.2. Параллельная коррекция.
По передаточной функции разомкнутой скорректированной системы строим действительную диаграмму Боде (рисунок 3.6.2):
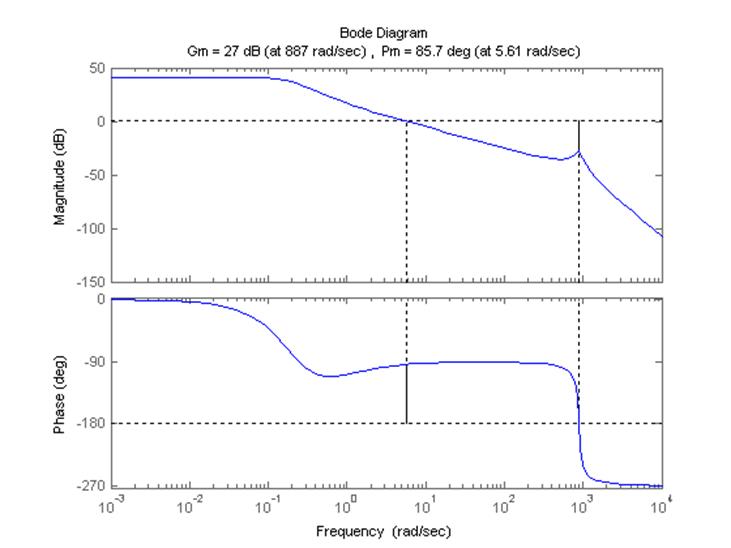
Рисунок 3.6.2. – ЛФЧХ разомкнутой скорректированной системы.
Из рисунка видно, что данная система является устойчивой.
Реальные запасы устойчивости составляют:
по фазе: 85.7º, по амплитуде: 27 дБ.
Для структурно-параметрическо синтеза САУ воспользуемся принципом подчиненного регулирования [2, с. 253].
Представим исходную структуру в виде двухконтурной системы, содержащей контуры тока и скорости (рис. 3.7.1.).
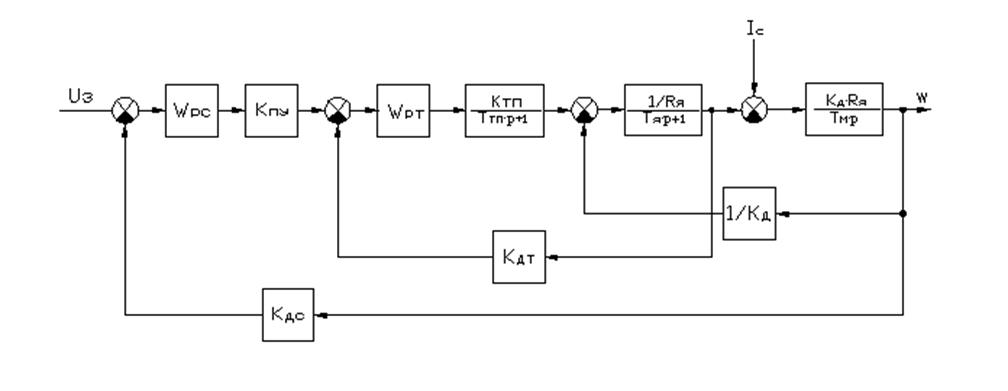 Рисунок
3.7.1 – Схема для структурно-параметрического синтеза.
Рисунок
3.7.1 – Схема для структурно-параметрического синтеза.
Для синтеза регуляторов на основе системы подчинённого регулирования пренебрегаем противо-ЭДС двигателя [2]. В соответствии с данной схемой находим передаточную функцию контура тока в разомкнутом состоянии:
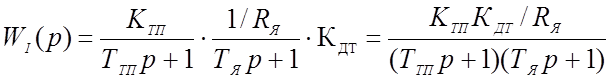
Для контура тока целесообразно применять ПИ-регулятор с настройкой на модульный оптимум (ТЯ=4ТТП):
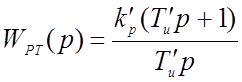
Вычисляем параметры регулятора (КДТ=0.08):
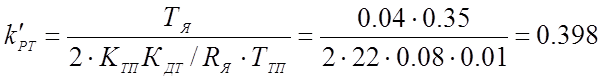
![]() с
с
Передаточная функция ПИ-регулятора тока:
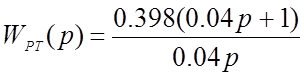
Передаточная функция контура тока в замкнутом состоянии с учётом регулятора тока:
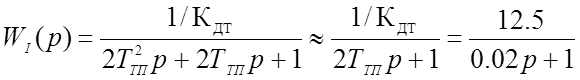
Производим настройку контура скорости. Передаточная функция разомкнутого контура скорости с учётом регулятора тока:
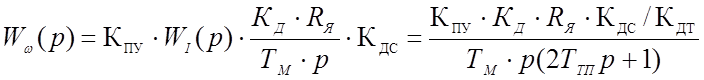
Применяем ПИ-регулятор, настроенный на симметричный оптимум с параметрами:
![]() с
с
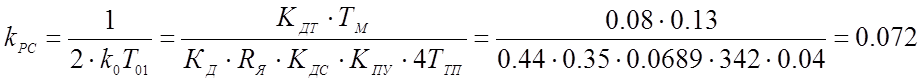 Передаточная
функция регулятора скорости:
Передаточная
функция регулятора скорости:
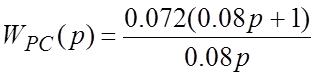
Для данных настроек контуров построим переходный процесс скорости для замкнутой системы для выяснения величины перерегулирования (представлен на рисунке 3.7.2).
По данной переходной характеристике видно, что перерегулирование чрезмерно велико (больше 25%). Следовательно, необходимо применение фильтра на входе системы для уменьшения перерегулирования.
Применяем сглаживающий фильтр с передаточной функцией:
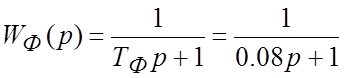
Переходный процесс скорости для данной системы с фильтром представлен на рисунке 3.7.3. По данному переходному процессу видно, что перерегулирование и время переходного процесса находятся в допустимых пределах.
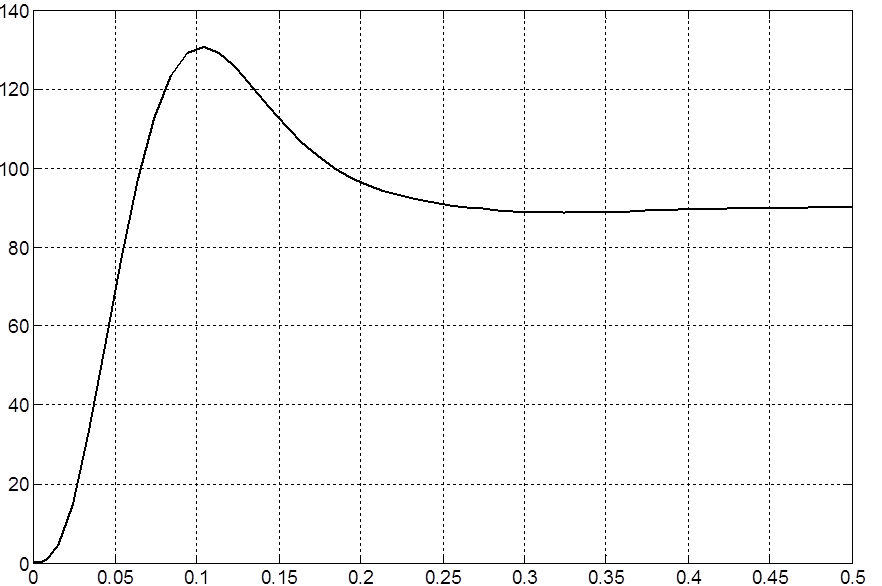
Рисунок 3.7.2 – Переходный процесс скорости в замкнутой системе
подчинённого регулирования с ПИ-регулятором скорости
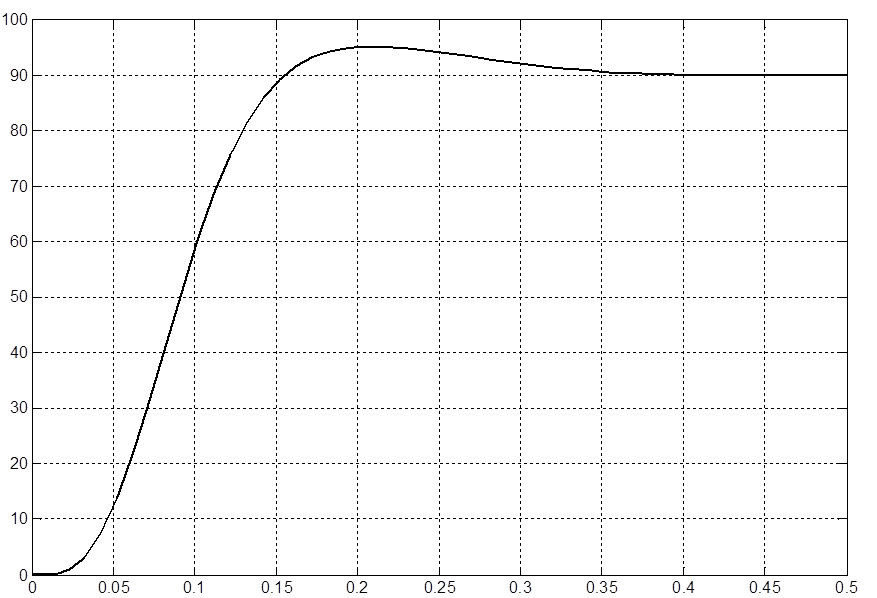
Рисунок 3.7.3 – Переходный процесс скорости в замкнутой системе
подчинённого регулирования с ПИ-регулятором скорости и фильтром
Выбор схем реализации регуляторов и фильтра.
1. Регулятор тока имеет следующую передаточную функцию:
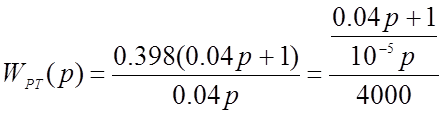
Схемная реализация регулятора тока [4]:
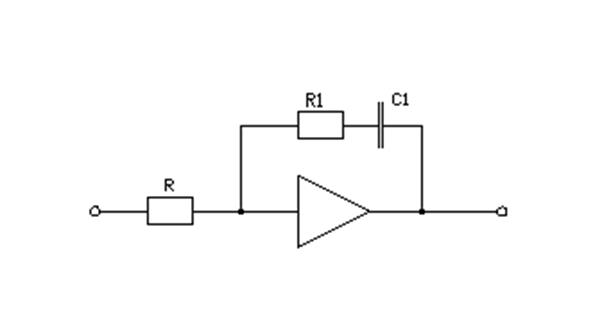
Рассчитываем параметры данной схемы:
Параметры входной цепи:
![]()
![]() кОм.
кОм.
Параметры цепи обратной связи:
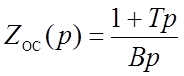 (
(![]() с)
с)
![]() мкФ;
мкФ;
![]()
![]() кОм.
кОм.
2. Регулятор скорости имеет передаточную функцию:
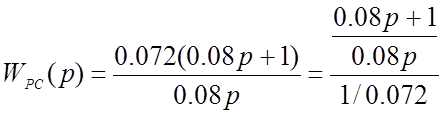
Для данного регулятора определяем схемную реализацию:
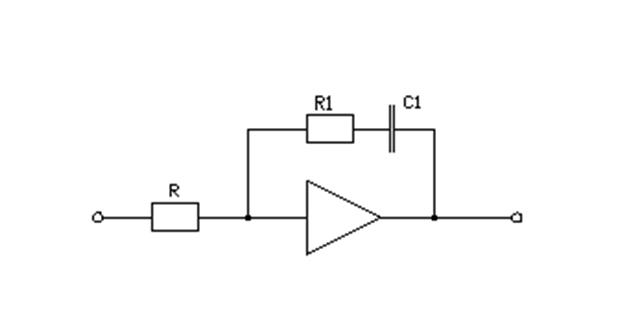
Рассчитываем параметры данной схемы:
Параметры входной цепи:
![]()
![]() кОм.
кОм.
Параметры цепи обратной связи:
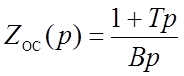 (
(![]() с)
с)
![]() мкФ;
мкФ;
![]()
![]() кОм.
кОм.
3. Сглаживающий фильтр имеет передаточную функцию:
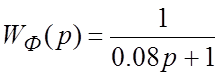
Для данного регулятора определяем схемную реализацию:
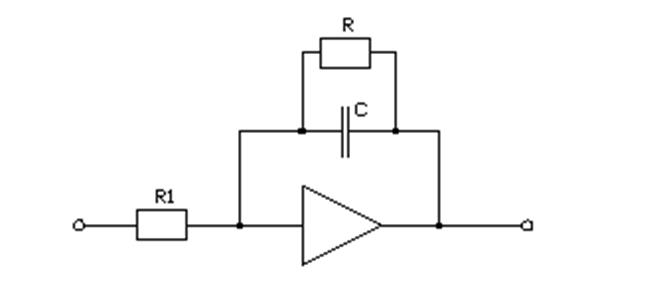
Рассчитываем параметры данной схемы:
Параметры входной цепи:
![]()
![]()
![]() кОм
кОм
Параметры цепи обратной связи:
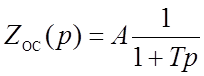 (
(![]() с)
с)
![]()
![]()
![]() кОм,
кОм,
![]() мкФ.
мкФ.
САУ с последовательной коррекцией
Строим переходные процессы скорости и тока от времени по управляющему воздействию:
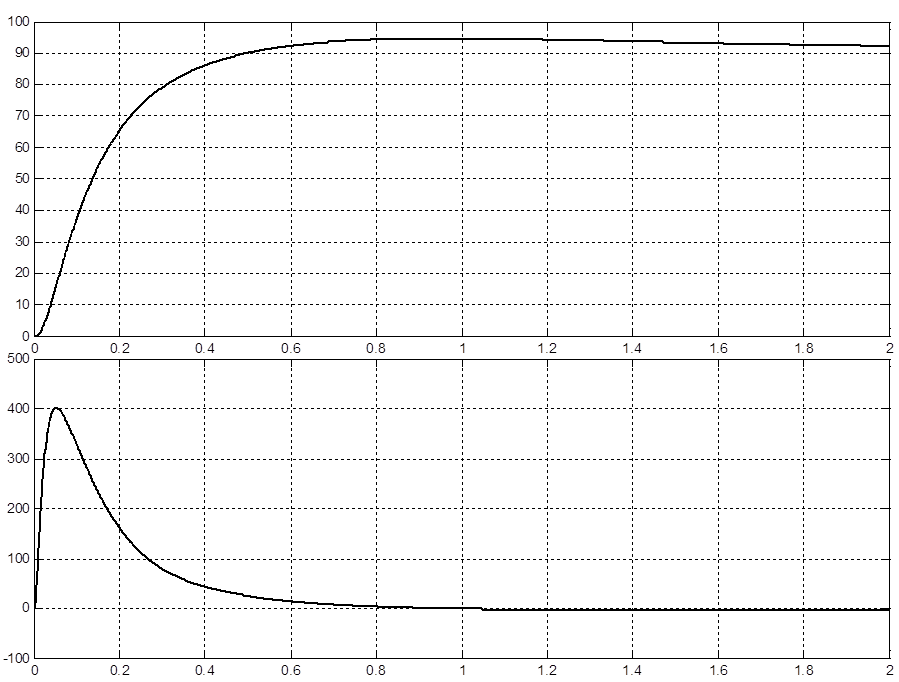
Рисунок 4.1.1 – Переходные процессы скорости и тока
по управляющему воздействию
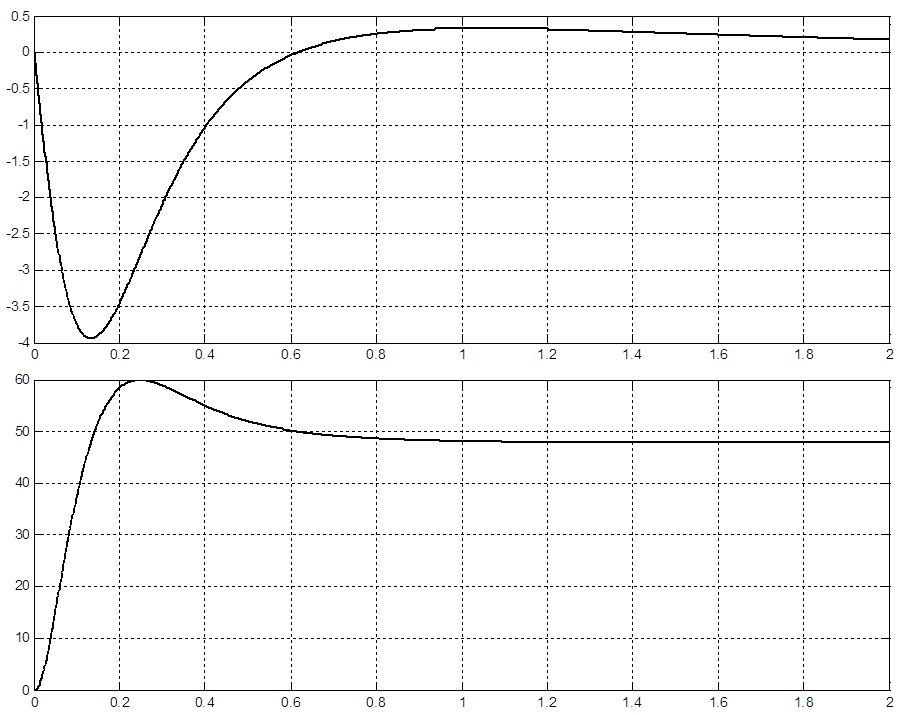
Строим переходные процессы скорости и тока от времени по возмущающему воздействию:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.