Расчет системы автоматического управления электроприводом при диапазоне регулирования D = 60 и перерегулировании скорости: σ = 25 %, страница 3

          Условием устойчивости системы для корневого годографа является то, что ветви годографа должны начинаться в полуплоскости с отрицательной действительной частью и, переходя в полуплоскость с положительной действительной частью, уходить в бесконечность. На пересечении ветвей годографа и оси ординат лежит критическое значение коэффициента усиления системы [1]. Вправо от оси ординат лежат значения коэффициента усиления системы, при которых система будет неустойчивой, а слева, соответственно, значения, при которых система будет устойчива.

          По рисунку 2.3.1 определим критическое значение коэффициента усиления разомкнутой системы:

К_КР = К*0.0709 = 228.1*0.0709=16.17

          Таким образом при К < 16.17 система будет устойчива.

          Так как (система неустойчива), следовательно, для достижения заданной точности регулирования необходимо скорректировать систему так, чтобы она была устойчивой.

2.4. Построение и анализ диаграммы Боде
для разомкнутой САУ.

          Строим диаграмму Боде для разомкнутой системы:

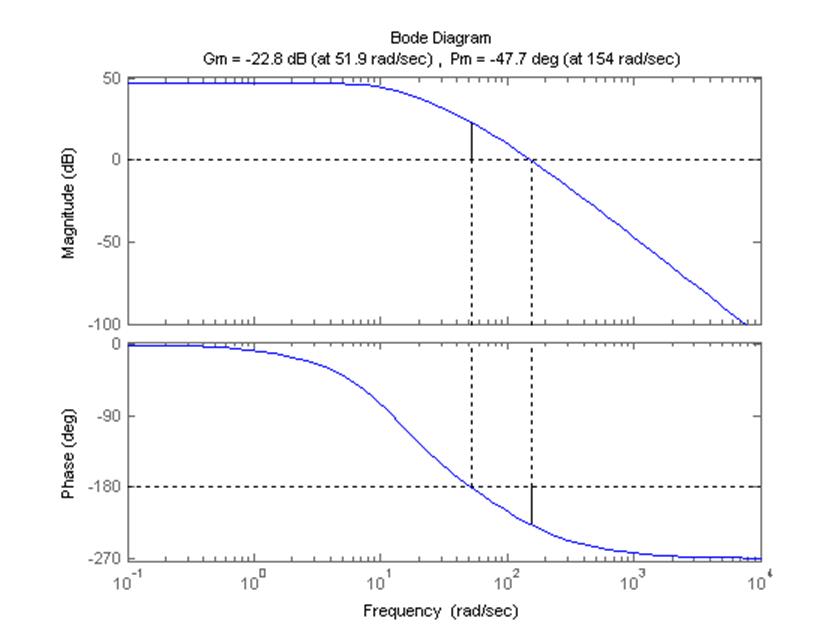
Рисунок 2.4.1 – Диаграмма Боде для разомкнутой системы.

          Из диаграммы Боде также видно, что система неустойчива, так как при достижении ФЧХ –180^о ЛАХ положительна [2, с.177] (запасы устойчивости отрицательны).

По ЛАХ определяем критический коэффициент передачи разомкнутой системы:

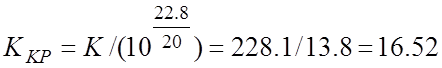
          Данный критический коэффициент усиления разомкнутой системы  практически совпадает с коэффициентом, найденным по корневому годографу. Система устойчива при К < 16.52.

          По виду ЛАХ можно определить:

1)  так как первоначальный наклон характеристики равен нулю, то система является статической;

2)  наклон характеристики в зоне частоты среза: -22.8/((154-51.9)/10) = -2.3 Б/дек = -23 дБ/дек, следовательно, система не имеет колебательности [3, с. 209];

3)  система имеет отрицательный запас устойчивости по фазе (-47.7°) и по амплитуде (-22.8 дБ).

2.5. Выводы по анализу устойчивости САУ.

          Исходная система является неустойчивой. Для обеспечения устойчивости требуется снизить коэффициент передачи разомкнутой системы (тогда она не будет удовлетворять заданным требованиям устойчивости) или ввести корректирующие звенья.

3. Синтез САУ.

3.1 Выбор и обоснование методов синтеза.

          Для синтеза корректирующего устройства выбираем методы последовательной и параллельной коррекции. Используя ЛАХ нескорректированной системы и желаемую ЛАХ, соответствующую заданному переходному процессу, определим тип и параметры корректирующего устройства. При выборе наилучшей из синтезированных САУ будем использовать ту, у которой наиболее простой вид корректирующего устройства. Для конечной скорректированной САУ должно выполняться условие реализуемости корректирующего устройства (степень числителя передаточной функции должна быть меньше или равна степени знаменателя).

3.2. Расчёт и построение асимптотической ЛАХ
исходной САУ и желаемой ЛАХ.

          Для построения асимптотической ЛАХ используем передаточную функцию разомкнутой системы по управляющему воздействию:

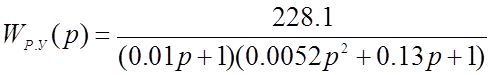
Постоянные времени данной системы:

с;   с.

          По данной передаточной функции рассчитываем положение асимптотических участков:

1) низкочастотный участок горизонтален (так как система статическая), начальное положение дБ. Этот участок располагается до частоты  рад/с.

          2)  среднечастотный участок имеет наклоном – 40 дБ/дек и  располагается между частотами  рад/с и  рад/с.

          3)   высокочастотный участок с наклоном – 60 дБ/дек располагается после частоты  рад/с.

Для построения фазовой частотной характеристики по ПФ разомкнутой системы найдем уравнение ФЧХ.

Коэффициент демпфирования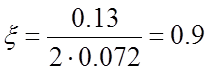

При 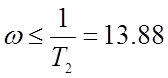рад/с:

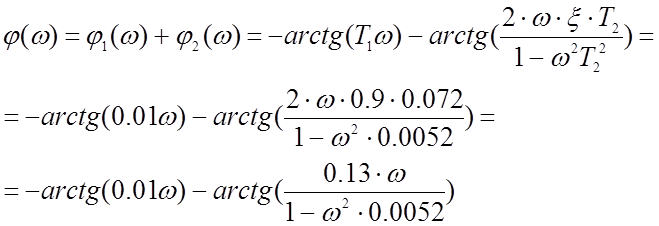
При 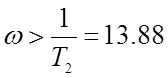рад/с:

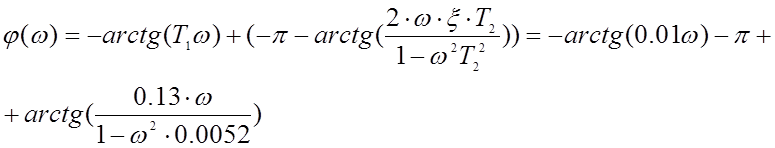
Для построения ЛАХ скорректированной системы определяем желаемую частоту среза системы (σ = 25% , t_ПП=2 с).