Проектирование и расчет систем автоматического управления при диапазоне регулирования D = 20, страница 3

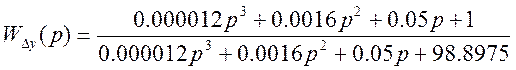
          6) Передаточная функция по ошибке от возмущающего воздействия:

1.5. Выводы по проведённому анализу.

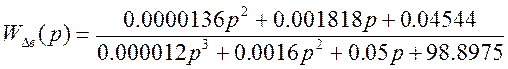
По полученным передаточным функциям можно сделать следующие выводы:

– знаменатели передаточных функций разомкнутых систем по управляющему и возмущающему воздействию равны;

– знаменатели передаточных функций замкнутых систем по управляющему и возмущающему воздействию, а так же знаменатели передаточных функций ошибки от управляющего и возмущающего воздействия, равны;

– по виду знаменателей всех полученных передаточных функций нельзя сказать об устойчивости системы, так как отсутствуют отрицательные члены в характеристических полиномах.

          Исходная система является статической как по управляющему, так и по возмущающему воздействию, в передаточных функциях разомкнутой системы по управляющему и по возмущающему воздействию отсутствует звено чистого интегрирования.

          По передаточным функциям замкнутой системы можно вычислить статическую ошибку системы, по передаточной функции (5) находим статическую ошибку от управляющего воздействия:

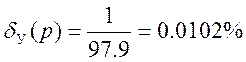
Данная ошибка удовлетворяет заданной (2%).

2. Анализ устойчивости САУ.

2.1. Анализ устойчивости замкнутой САУ
с помощью алгебраического критерия.

Для определение устойчивости САУ по критерию Гурвица необходимо составить характеристического уравнения замкнутой САУ.

Характеристическое уравнение замкнутой САУ имеет вид:

     (3.1)

По критерию Гурвица для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель были положительными.

Подставив исходные данные в формулу, получим:

                                           (3.2)

Kпу=146,89;

                                                             (3.3)

                                                                                                   (3.4)

                                                                                                            (3.5)

Так как определители   и  меньше нуля, то система не устойчива.

2.2. Анализ устойчивости с использованием
частотного критерия.

Критерий Найквиста позволяет судить об устойчивости системы по амплитудной – фазовой характеристики разомкнутого контура системы.

Для устойчивости  системы по критерию Найквиста необходимо и достаточно, чтобы амплитудно – фазовая характеристика разомкнутого контура не охватывала точку с координатами (-1; j0).

Передаточная функция САУ:

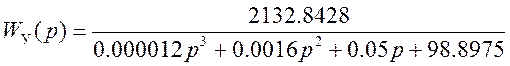
          Передаточная функция разомкнутого контура:

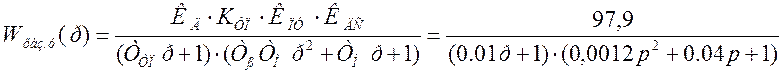
          С помощью программы MATLAB строим диаграмму Найквиста:

>> nyquist(W)

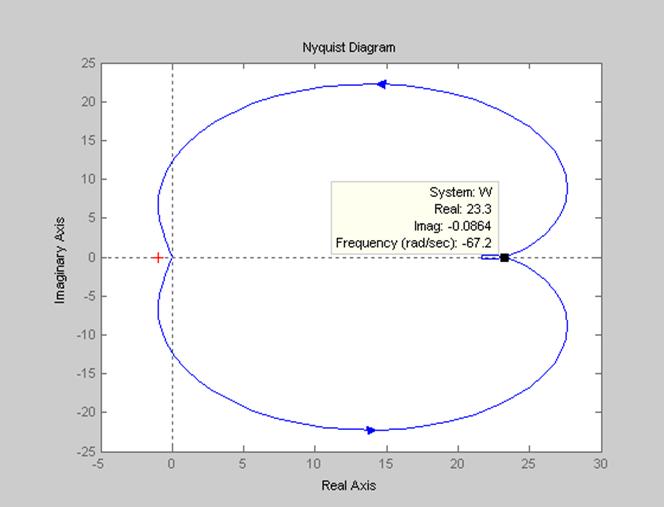
Рисунок 2 – Диаграмма Найквиста разомкнутого контура

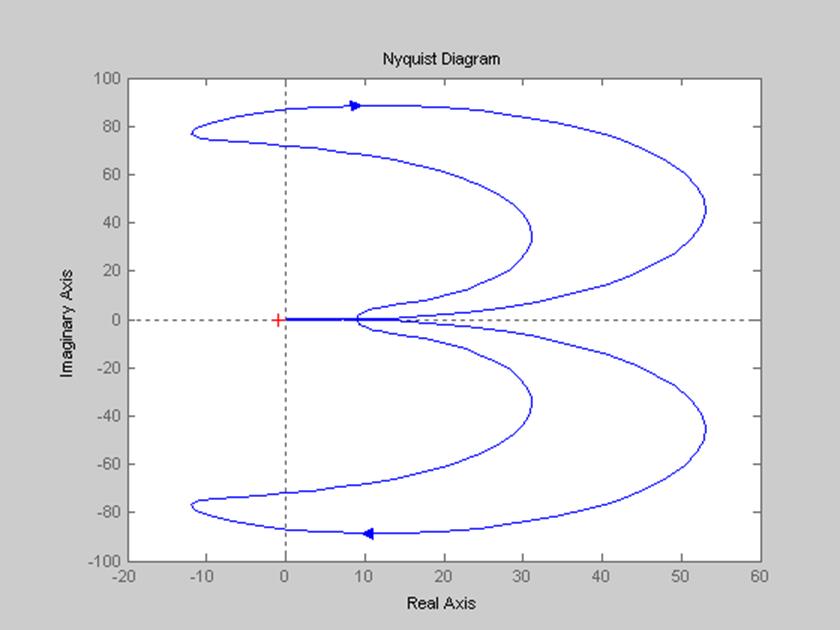
Рисунок 3 – Годограф Найквиста вблизи точки (-1;j0)

По данному годографу видно, что он охватывает точку (-1; 0). Условием же устойчивости системы является условие не охвата годографом данной точки. Значит, данная система не устойчива.

2.3. Анализ влияния коэффициента усиления
разомкнутой САУ на устойчивость.

Определим диапазон значений коэффициента усиления разомкнутой системы в котором она будет устойчива в замкнутом состоянии.

Для определения критического коэффициента воспользуемся методом корневого годографа.

Передаточная функция САУ:

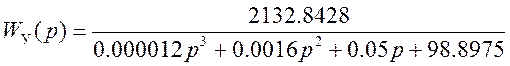
Передаточная функция разомкнутой САУ:

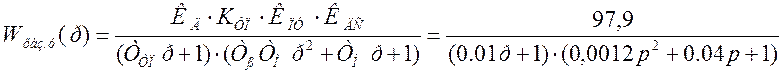
С помощью программы MATLAB строим корневой годограф разомкнутой САУ:

>> rlocus(W)

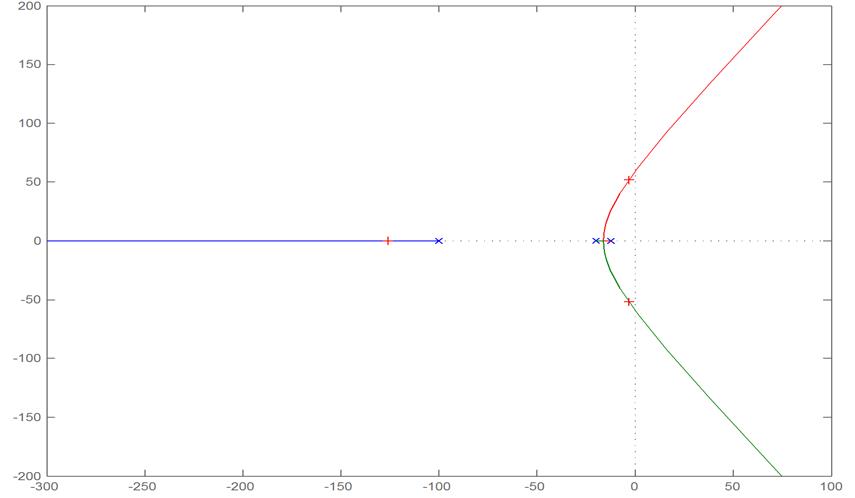
Рисунок 4 – Корневой годограф передаточной функции  разомкнутой САУ

Условием устойчивости системы для корневого годографа является то, что ветви годографа должны начинаться в полуплоскости с отрицательной действительной частью и переходя в полуплоскость с положительной действительной частью уходить в бесконечность. На пересечении ветвей годографа и оси ординат лежит критическое значение коэффициента усиления системы. Вправо от оси ординат лежат значения коэффициента усиления системы, при которых система будет неустойчивой, а слева, соответственно, значения, при которых система будет устойчива.

          По данному годографу определим критическое значение коэффициента усиления разомкнутой системы: