Исследование звена второго порядка. Исследование характеристик заграждающего фильтра. Исследование характеристик неминимально-фазового звена

Федеральное агентство по образованию

Государственное образовательное учреждение
высшего профессионального образования

“Сибирский государственный индустриальный университет”

Кафедра АЭП и ПЭ

Отчет по лабораторной работе

               Выполнил:  студент гр. АЭП-081

                  Александров А.А.

                   Селезнёв А. Ю.

                    Орлов Э.С

               Принял:  Петрашов  В.П.

Новокузнецк, 2011 г.

Исследование звена второго порядка

>> w0=10; k1=0; k2=0.1; k3=0.5; k4=1; T=1/w0;

Получение передаточных функции:

w1=tf([1],[T^2 2*k1*T 1])

Transfer function:

        1

-----------------

0.0001563 s^2 + 1

w2=tf([1],[T^2 2*k2*T 1])

Transfer function:

             1

----------------------------

0.0001563 s^2 + 0.0025 s + 1

w3=tf([1],[T^2 2*k3*T 1])

Transfer function:

             1

----------------------------

0.0001563 s^2 + 0.0125 s + 1

w4=tf([1],[T^2 2*k4*T 1])

Transfer function:

             1

---------------------------

0.0001563 s^2 + 0.025 s + 1

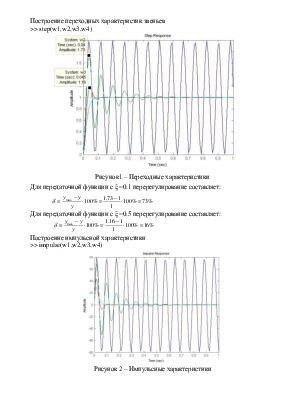
Построение переходных характеристик звеньев

>> step(w1,w2,w3,w4)

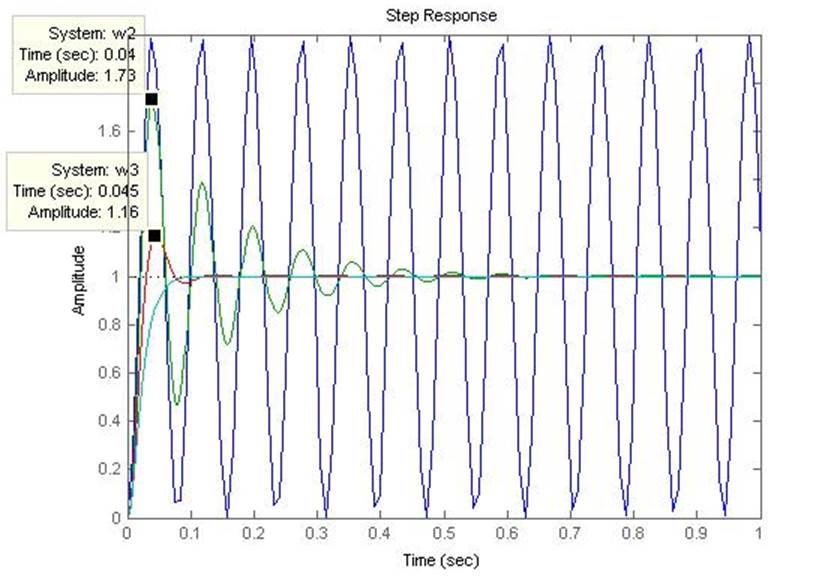
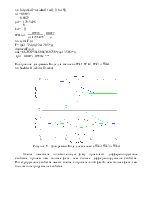
Рисунок1 – Переходные характеристики

Для передаточной функции с ξ =0.1 перерегулирование составляет:

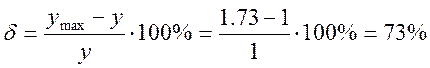
Для передаточной функции с ξ =0.5 перерегулирование составляет:

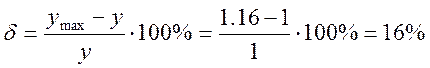
Построение импульсной характеристики

>> impulse(w1,w2,w3,w4)

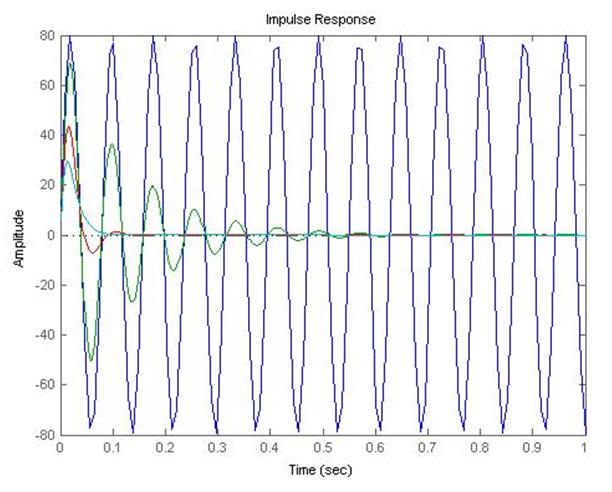
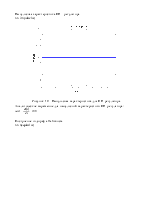
Рисунок 2 – Импульсные характеристики

Получение аналитического выражения звена при k=0.1

>> [r1,p1,kk1]=residue([1],[T^2 2*k2*T 1])

r1 =

        0 -40.2015i

        0 +40.2015i

p1 =

  -8.0000 +79.5990i

  -8.0000 -79.5990i

kk1 =   []

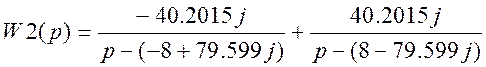
>> syms F p t

F=1/(1/6400*p^2+0.0025*p+1);

ilaplace(F,p,t)

ans =800/33*11^(1/2)*exp(-8*t)*sin(24*11^(1/2)*t)

Т.о. аналитическое выражение звена будет иметь вид:

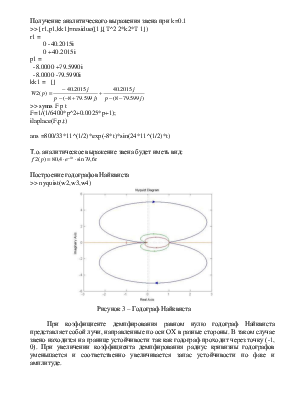
Построение годографов Найквиста

>> nyquist(w2,w3,w4)

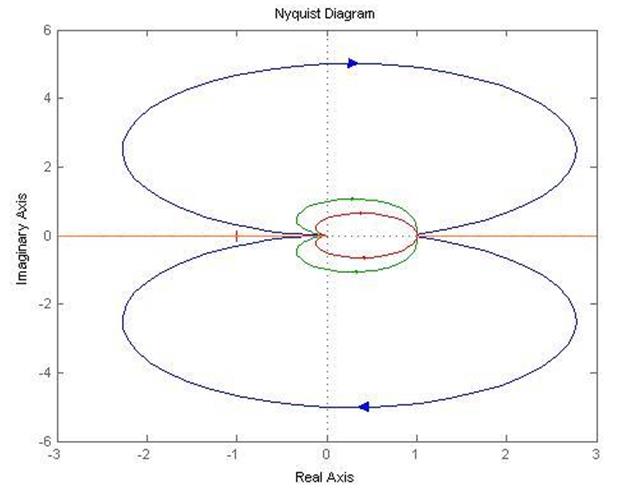
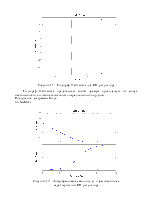
Рисунок 3 – Годограф Найквиста

При коэффициенте демпфирования равном нулю годограф Найквиста представляет собой лучи, направленные по оси ОХ в разные стороны. В таком случае звено находится на границе устойчивости так как годограф проходит через точку (-1, 0). При увеличении коэффициента демпфирования радиус кривизны годографов уменьшается и соответственно увеличивается запас устойчивости по фазе и амплитуде.

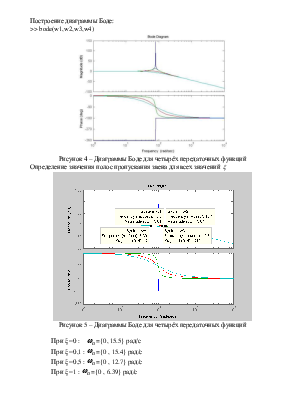
Построение диаграммы Боде:

>> bode(w1,w2,w3,w4)

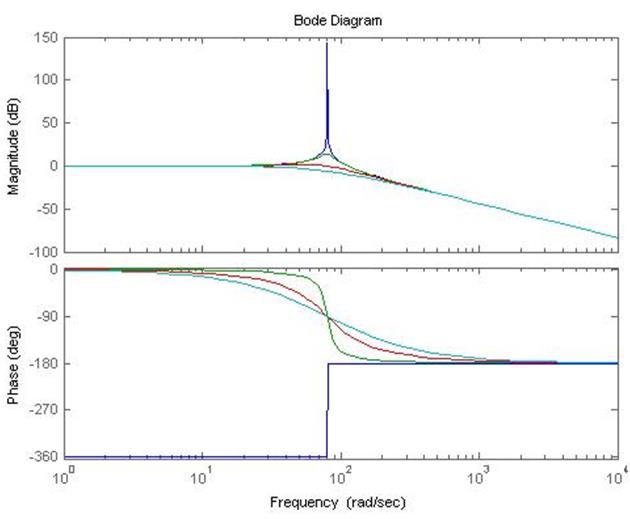
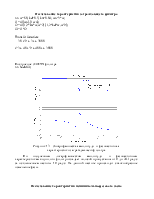
Рисунок 4 – Диаграммы Боде для четырёх передаточных функций

Определение значения полос пропускания звена для всех значений

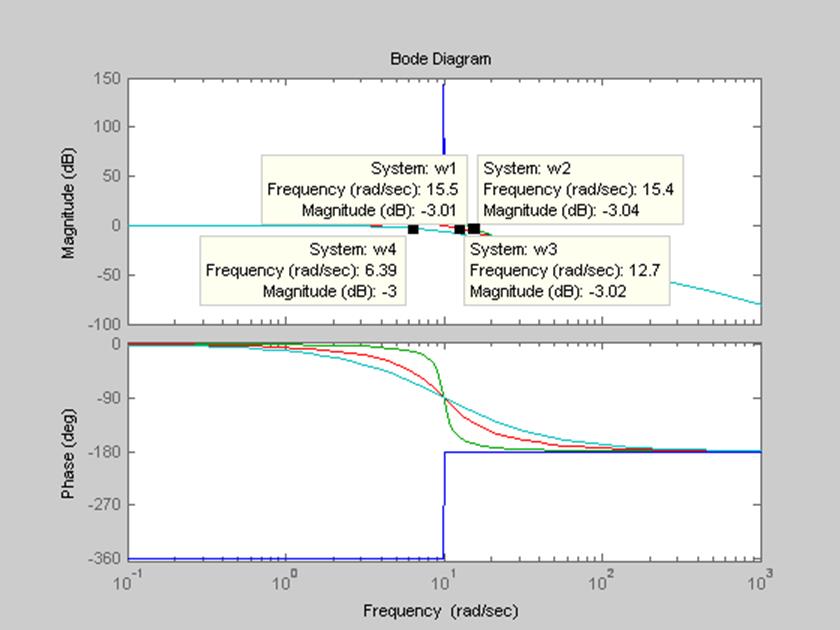
Рисунок 5 – Диаграммы Боде для четырёх передаточных функций

При ξ =0 :    ={0, 15.5} рад/с

При ξ =0,1 : ={0 , 15.4} рад/с

При ξ =0,5 : ={0 , 12.7} рад/с

При ξ =1 : ={0 , 6.39} рад/с

Чем выше значение коэффициента демпфирования, тем меньше полоса пропускания w, следовательно меньше интервал частот, при котором амплитуда меньше начального значения на 3дБ.

Исследование корректирующего звена

>> w=5; fi1=-80; fi2=-30; fi3=30;fi4=80;

a1=-w*pi*(tan(fi1*pi/180)-sec(fi1*pi/180));

a2=-w*pi*(tan(fi2*pi/180)-sec(fi2*pi/180));

a3=-w*pi*(tan(fi3*pi/180)-sec(fi3*pi/180));

a4=-w*pi*(tan(fi4*pi/180)-sec(fi4*pi/180));

b1=w*pi*(tan(fi1*pi/180)+sec(fi1*pi/180));

b2=w*pi*(tan(fi2*pi/180)+sec(fi2*pi/180));

b3=w*pi*(tan(fi3*pi/180)+sec(fi3*pi/180));

b4=w*pi*(tan(fi4*pi/180)+sec(fi4*pi/180));

wk1=tf([1 a1],[1 b1])

Transfer function: Transfer function:

s + 359.1

---------

s + 2.749

>> wk2=tf([1 a2],[1 b2])

Transfer function:

s + 54.41

---------

s + 18.14

>> wk3=tf([1 a3],[1 b3])

Transfer function:

s + 18.14

---------

s + 54.41

>> wk4=tf([1 a4],[1 b4]

Transfer function:

s + 2.749

---------

s + 359.1

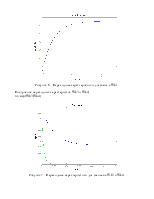
Построение переходных характеристик Wk1, Wk2;

>> step(Wk1,Wk2)

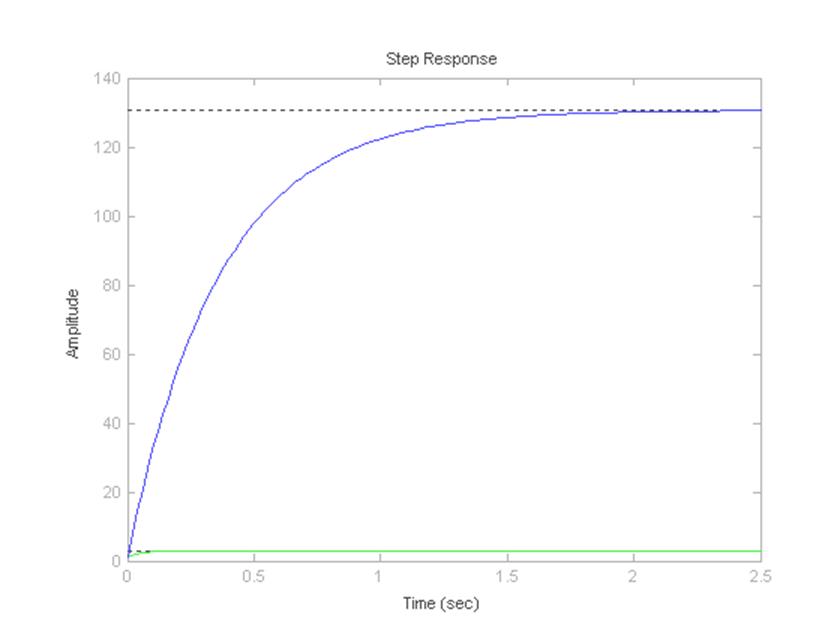
Рисунок 6 – Переходные характеристики для звена с Wk1

Построение переходных характеристик Wk3 и Wk4;

>> step(Wk3,Wk4)

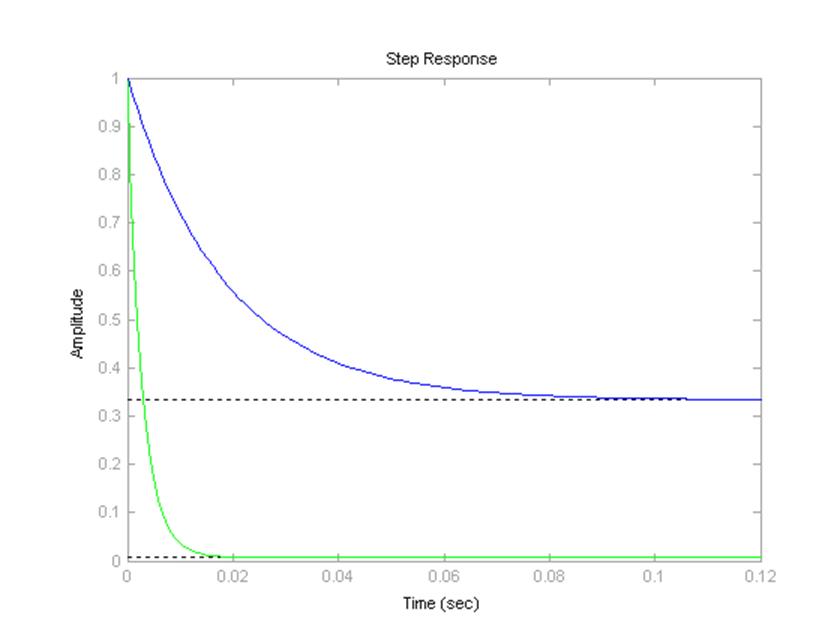
Рисунок 7 – Переходные характеристики для звеньев с Wk3 и Wk4

Определение аналитических выражений переходных характеристик:

>> [r1,p1,k1]=residue([1 a1], [1 b1 0])

r1 = -129.6461

         130.6461

p1 = -1.3743

         0

k1 =   []

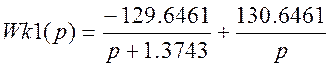
>> syms F p t

F=(p+179.5)/(p^2+1.374*p)

ilaplace(F,p,t)

ans=89750/687-89063/687*exp(-687/500*t)

>> [r2,p2,k2]=residue([1 a2], [1 b2 0])

r2 = -2.0000

         3.0000

p2 = -9.0690

           0

k2 =  []

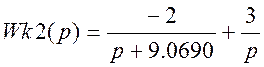
>> syms F p t

F = (p+27.21)/(p^2+9.069*p)

ilaplace(F,p,t)

ans =9070/3023-6047/3023*exp(-9069/1000*t)

>> [r3,p3,k3]=residue([1 a3], [1 b3 0])

r3 =0.6667

      0.3333

p3 =-27.2070

         0

k3 = []

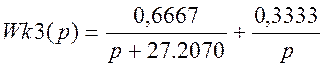
>> syms F p t

F= (p+9.069)/(p^2+27.21*p)

ilaplace(F,p,t)

ans =3023/9070+6047/9070*exp(-2721/100*t)