Исследование звена второго порядка. Исследование характеристик заграждающего фильтра. Исследование характеристик неминимально-фазового звена, страница 2

>> [r4,p4,k4]=residue([1 a4], [1 b4 0])

r4 =0.9923

      0.0077

p4 = -179.5428

         0

k4 =   []

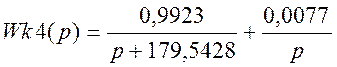
>> syms F p t

F= (p+1.374)/(p^2+179.5*p)

ilaplace(F,p,t)

ans =687/89750+89063/89750*exp(-359/2*t)

Построение диаграммы Боде для звеньев с Wk1, Wk2, Wk3 и Wk4.

>> bode(wk1,wk2,wk3,wk4)

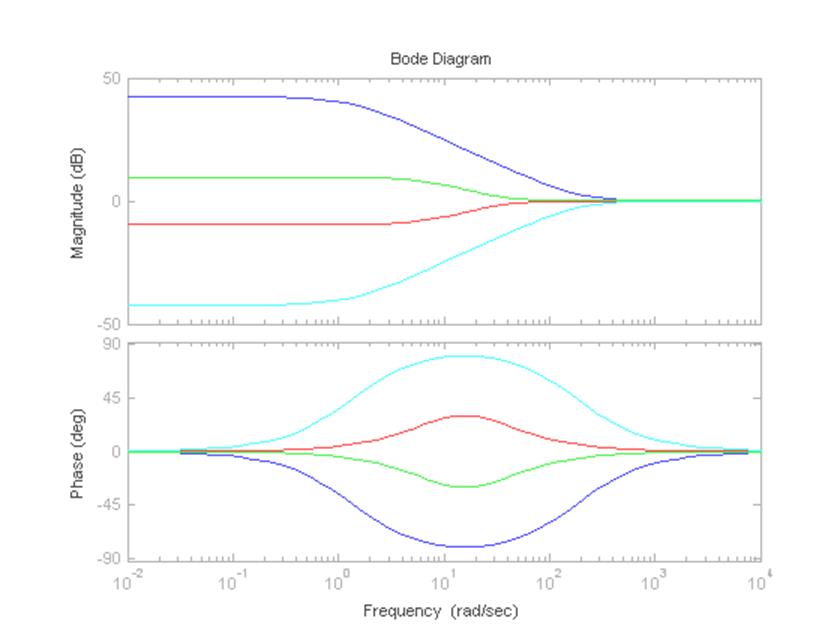
Рисунок 8 – Диаграммы Боде для звеньев с Wk2, Wk3 и Wk4

Звенья имеющие положительную фазу проявляют дифференцирующие свойства, причём чем больше фаза, тем больше дифференцирующие свойства. Интегрирующие свойства имеют звенья с отрицательной фазой, чем больше фаза, тем больше интегрирующие свойства.

Исследование ПИ – регулятора

>> kp=1; Tp=0.01

w=tf([kp*Tp kp],[Tp 0])

Transfer function:

0.01 s + 1

----------

  0.01 s

Построение переходной характеристики для ПИ – регулятора

>> step(w)

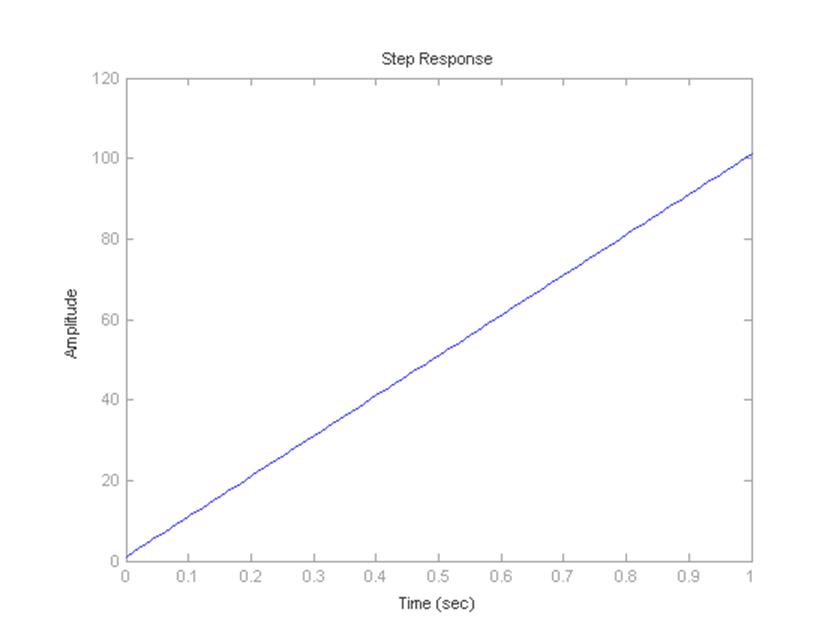
Рисунок 9 – Переходная характеристика для ПИ–регулятора

>> [r,p,k]=residue([28 35],[0.08 0 0])

r =10

    100

p = 0

      0

k = []

>> syms F p t

F=(0.01*p+1)/(0.01*p^2)

ilaplace(F,p,t)

ans =100*t+1

Аналитическое выражение для переходной характеристики ПИ–регулятора:

Импульсная характеристика ПИ – регулятора

>>  impulse(w)

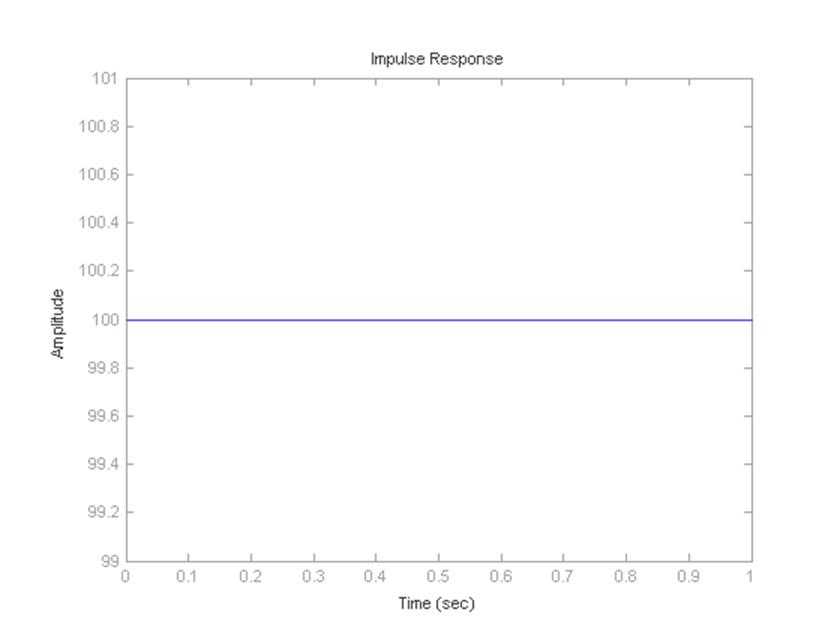
Рисунок 10 – Импульсная характеристика для ПИ–регулятора

Аналитическое выражение для импульсной характеристики ПИ–регулятора:

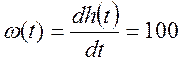
Построение годографа Найквиста

>> nyquist(w)

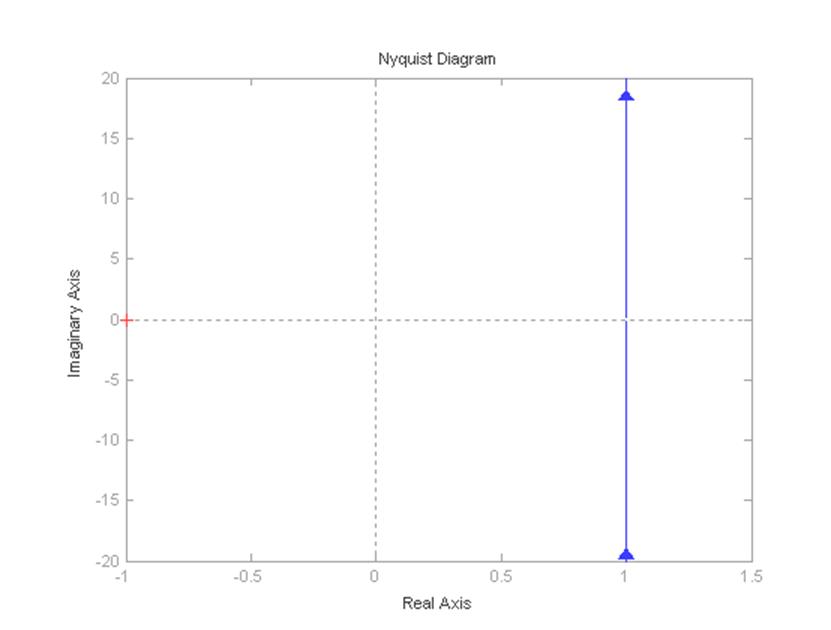
Рисунок 11 – Годограф Найквиста для ПИ–регулятора

Годограф Найквиста представляет собой прямую проходящую из минус бесконечности в плюс бесконечность параллельно оси ординат.

Построение диаграммы Боде:

>> bode(w)

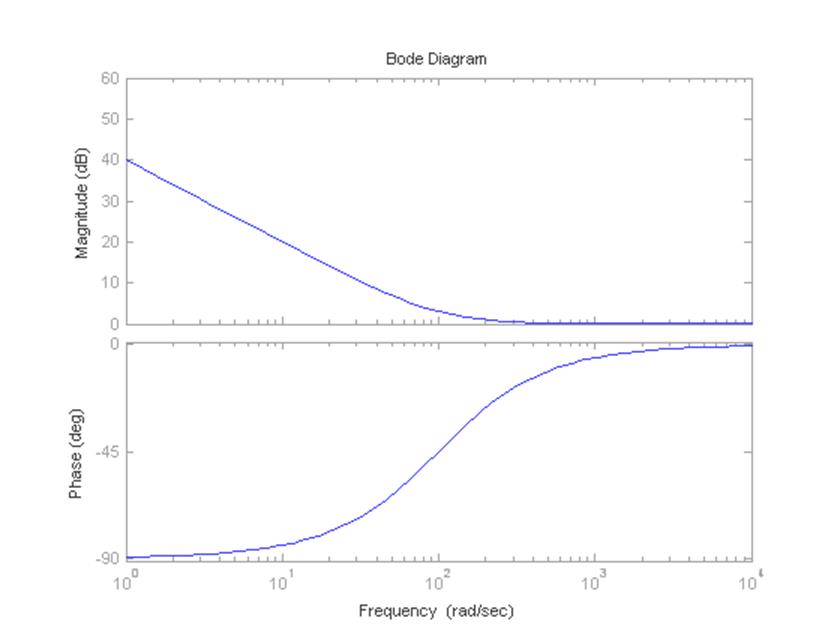
Рисунок 12 – Логарифмическая амплитудо- и фазочастотная
характеристики ПИ–регулятора

Исследование характеристик заграждающего фильтра

>> w=80; kd=0.5; kn=0.04; wa=3*w;

f1=tf([wa],[1,wa])

f2=tf([1,2*kn*w,w^2],[1,2*kd*w,w^2])

fil=f1*f2

Transfer function:

    30 s^2 + 3 s + 3000

---------------------------

s^3 + 40 s^2 + 400 s + 3000

Построение ЛАФЧХ фильтра

>> bode(fil)

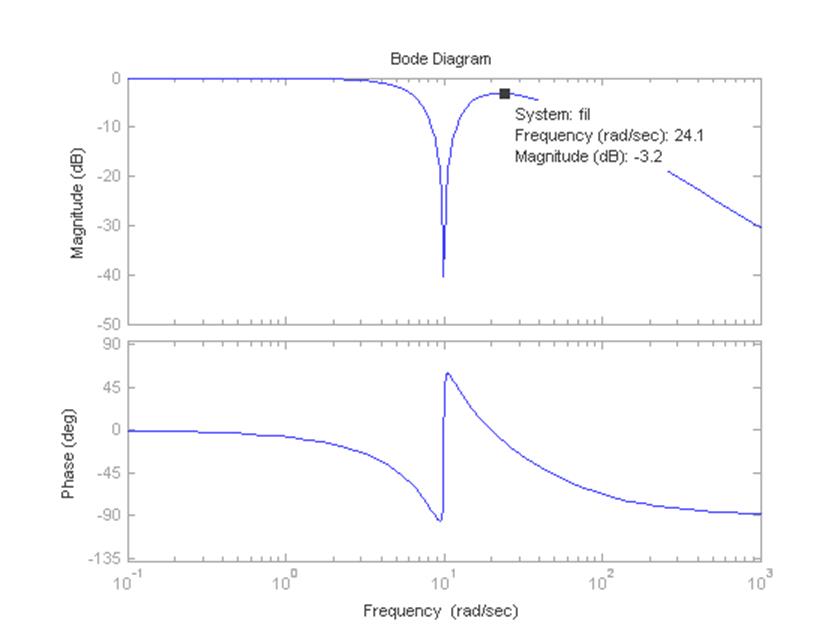
Рисунок 13 – Логарифмическая амплитудо- и фазочастотная
характеристики заграждающего фильтра

По полученным логарифмическим амплитудо- и фазочастотным характеристикам видно, что фильтр обладает полосой пропускания от 0 до 24.1 рад/с за исключением частоты 10 рад/с. На данной частоте происходит скачкообразное изменение фазы.

Исследование характеристик неминимально-фазового звена

>> w=5; fi1=-80; fi2=-30; fi3=30;fi4=80;

a1=-w*pi*(tan(fi1*pi/180)-sec(fi1*pi/180));

a2=-w*pi*(tan(fi2*pi/180)-sec(fi2*pi/180));

a3=-w*pi*(tan(fi3*pi/180)-sec(fi3*pi/180));

a4=-w*pi*(tan(fi4*pi/180)-sec(fi4*pi/180));

b1=w*pi*(tan(fi1*pi/180)+sec(fi1*pi/180));

b2=w*pi*(tan(fi2*pi/180)+sec(fi2*pi/180));

b3=w*pi*(tan(fi3*pi/180)+sec(fi3*pi/180));

b4=w*pi*(tan(fi4*pi/180)+sec(fi4*pi/180));

wk1=tf([1 -a1],[1 b1])

wk2=tf([1 -a2],[1 b2])

wk3=tf([1 -a3],[1 b3])

wk4=tf([1 -a4],[1 b4])

Transfer function:

s - 179.5

---------

s + 1.374

Transfer function:

s - 27.21

---------

s + 9.069

Transfer function:

s - 9.069

---------

s + 27.21

Transfer function:

s - 1.374

---------

s + 179.5

Передаточные характеристики неминимально-фазовых звеньев:

; ;  ;  .

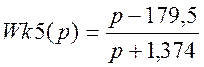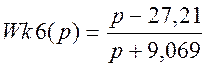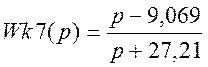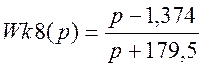>> step(wk5)

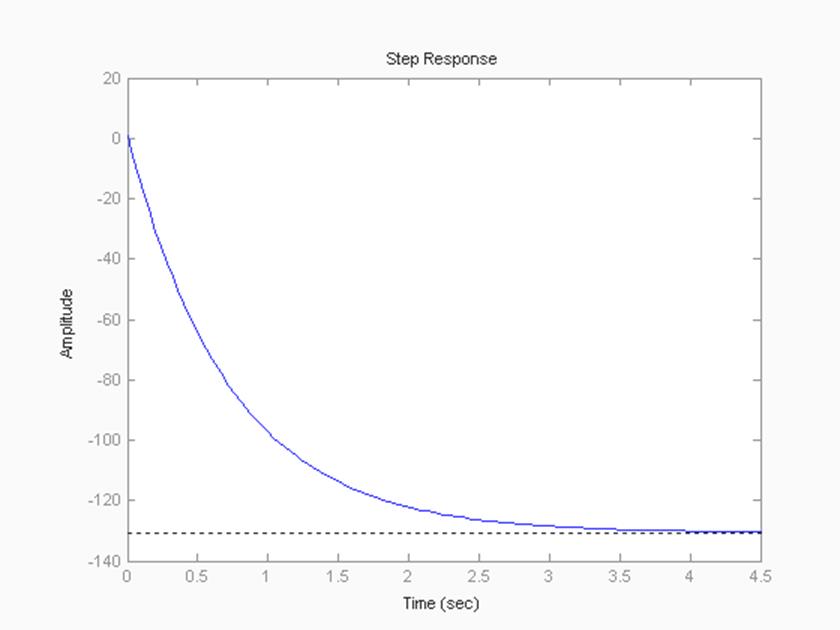
Рисунок 14 – Переходная характеристика для Wk5

>> step(wk6,wk7,wk8)

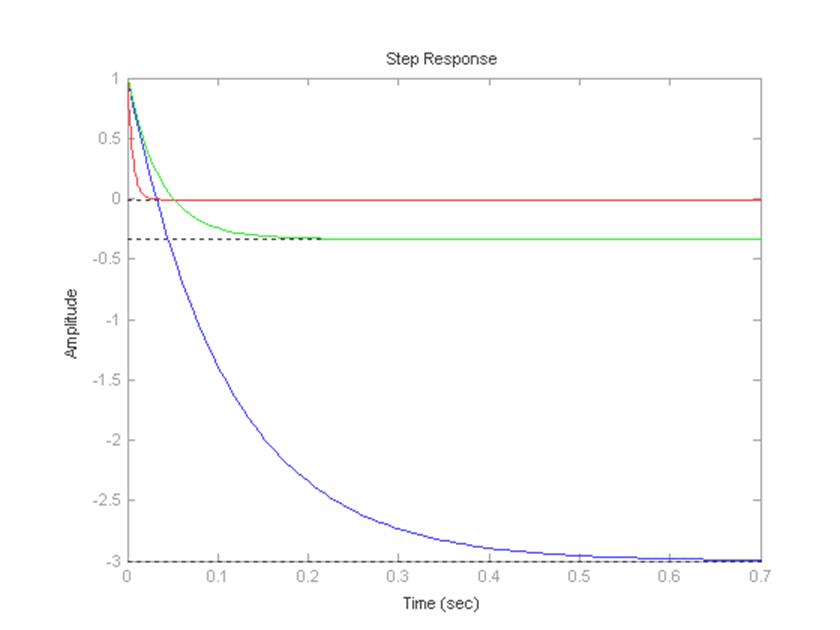
Рисунок 15 – Переходные характеристики для Wk6, Wk7 и Wk8

>> [r1,p1,k1]=residue([1 -a1], [1 b1 0])

r1 =131.6461

     -130.6461

p1 = -1.3743

         0

k1 =  []

>> syms F p t

F=(p-179.5)/(p^2+1.374*p)

ilaplace(F,p,t)

ans =-89750/687+90437/687*exp(-687/500*t)

>> [r2,p2,k2]=residue([1 -a2], [1 b2 0])

r2 =4

      -3

p2 = -9.0690

         0

k2 = []

>> syms F p t

F=(p-27.21)/(p^2+9.069*p)

ilaplace(F,p,t)

ans =-9070/3023+12093/3023*exp(-9069/1000*t)

>> [r3,p3,k3]=residue([1 -a3], [1 b3 0])

r3 =1.3333

     -0.3333

p3 = -27.2070

         0

k3 = []

>> syms F p t

F=(p-9.069)/(p^2+27.21*p)

ilaplace(F,p,t)

ans =-3023/9070+12093/9070*exp(-2721/100*t)

>> [r4,p4,k4]=residue([1 -a4], [1 b4 0])

r4 =  1.0077

        -0.0077

p4 = -179.5428

         0

k4 =  []

>> syms F p t

F=(p-1.374)/(p^2+179.5*p)

ilaplace(F,p,t)

ans =-687/89750+90437/89750*exp(-359/2*t)

Построение диаграмм Боде

>> bode(wk5,wk6,wk7,wk8)

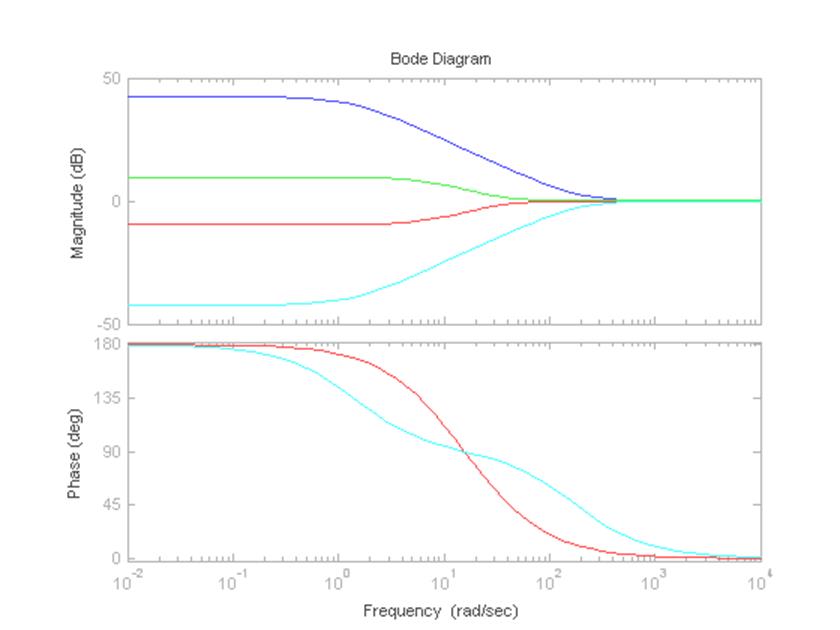
Рисунок 16 – Диаграммы Боде для неминимально-фазовых звеньев

ЛАФХ показывают, что неминимально-фазовые звенья могут иметь свойства как дифференцирующих, так и интегрирующих звеньев. ЛАХ неминимально-фазовых звеньев схожи с ЛАХ минимально-фазовых. ЛФХ неминимально-фазовых звеньев отличаются от ЛФХ минимально-фазовых.