Исследование устойчивости линейных непрерывных систем автоматического управления. Вариант № 1

Федеральное агентство по образованию

Государственное образовательное учреждение
высшего профессионального образования

“Сибирский государственный индустриальный университет”

Кафедра АЭП и ПЭ

Отчет по лабораторной работе № 2

Исследование устойчивости линейных непрерывных систем автоматического управления.

Вариант № 1

Выполнил:  студент гр. АЭП-042

Афанасьев Н.Ю.

Ручкин А.С.

Принял: к.т.н, доцент

Богдановская Т.В.

Новокузнецк, 2007 г.

Цель работы: освоение различных методов определения устойчивости САУ и их использование для выбора параметров, обеспечивающих устойчивую работу систем в различных режимах.

1.)  Проверка устойчивости замкнутой системы с помощью общего условия устойчивости и корневого годографа.

Заданная ПФ

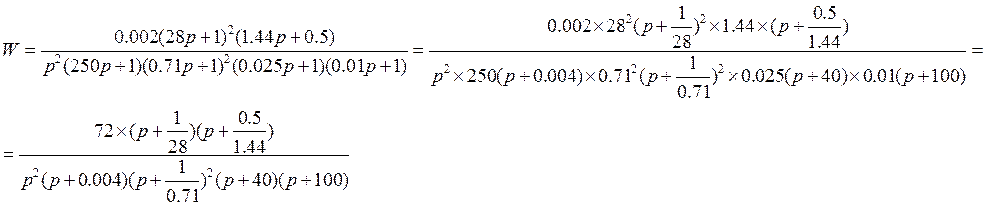
Передаточная функция разомкнутой системы:

>> W=zpk([-1/28 -1/28 -0.5/1.44],[0 0 -0.004 -1/0.71 -1/0.71 -40 -100],72)

Zero/pole/gain:

      72 (s+0.03571)^2 (s+0.3472)

----------------------------------------

s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

Определение нулей и полюсов передаточной функции:

>> tzero(W)

ans =   -0.0357

            -0.0357

            -0.3472

>> pole(W)

ans =  0    0    -0.0040    -1.4085    -1.4085    -40    -100

Введение замкнутой единичной обратной связи в заданную систему:

>> feedback(W,1)

Zero/pole/gain:

                           72 (s+0.3472) (s+0.03571)^2

---------------------------------------------------------------------------------

(s+100) (s+40) (s+0.01313) (s^2  - 0.005701s + 0.0003048) (s^2  + 2.813s + 1.992)

Построение корневого годографа:

>> rlocus(W)

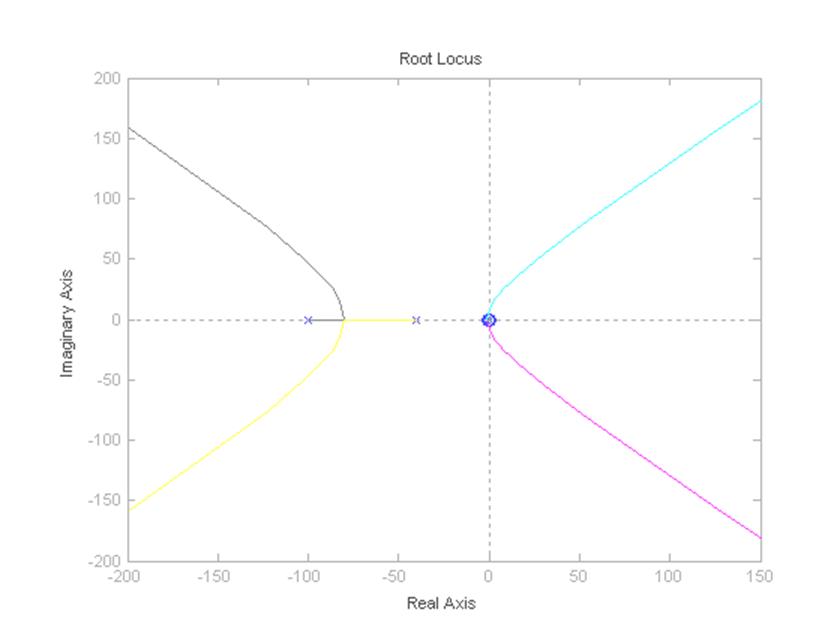
Рисунок 1 – Корневой годограф САУ

0.0002 < k <0.257  – диапазон значений коэффициента передачи разомкнутой системы, при котором система устойчива в замкнутом состоянии.

2.) Оценка устойчивости по ЛАФЧХ.

Построение диаграммы Боде для разомкнутой САУ с указанием запасов устойчивости (по амплитуде и по фазе):

>> margin(W)

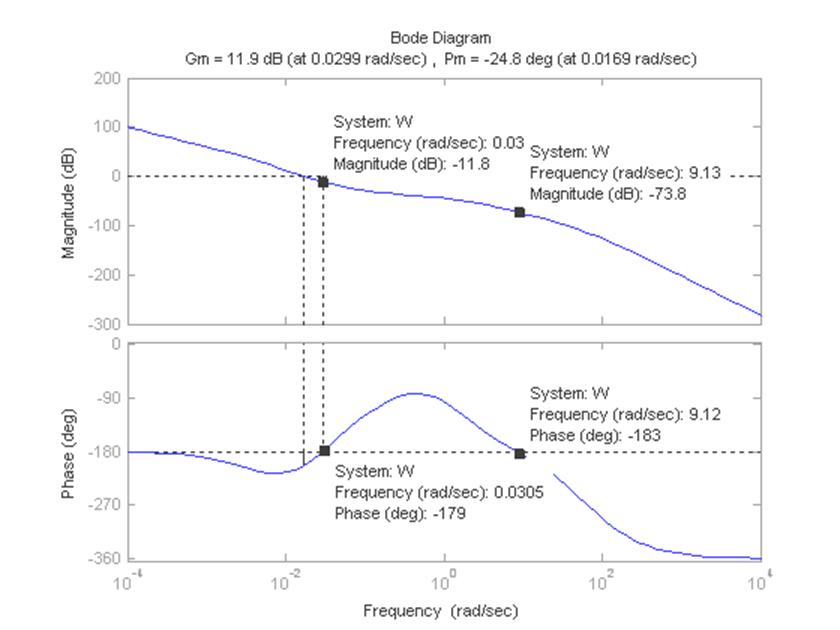
Рисунок 2 – Диаграмма Боде для разомкнутой САУ

По данным значениям критических коэффициентов определим области устойчивости:

Определение диапазона значений коэффициента передачи  k, в котором система будет устойчивой, по критерию Рауса.

 Передаточная функция разомкнутой системы:

                         72 (s+0.03571)^2 (s+0.3472)

Wp(P)=            ----------------------------------------

                     s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

Характеристическое уравнение замкнутой системы запишется:

                                72 (s+0.03571)^2 (s+0.3472)

Wp(P)=  1+          ----------------------------------------

                       s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

Данное характеристическое уравнение имеет высокий порядок, поэтому критерий Рауса в данном случае не применяется.

3.)  Исследование системы при значениях k, близких к критическим.

При kkp=3*kкрmin;

>> W1=W*3*3.891

Zero/pole/gain:

    840.456 (s+0.03571)^2 (s+0.3472)

----------------------------------------

s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

>> Wz1=feedback(W1,1)

Zero/pole/gain:

                        840.456 (s+0.3472) (s+0.03571)^2

--------------------------------------------------------------------------------

(s+100) (s+40.01) (s+0.0211) (s^2  + 0.02144s + 0.002119) (s^2  + 2.77s + 2.081)>>

tzero(Wz1)

ans =

         -0.3472

         -0.0357

         -0.0357

>> pole(Wz1)

ans =

 -99.9986         

 -40.0093         

  -1.3852 + 0.4028i

  -1.3852 - 0.4028i

  -0.0107 + 0.0448i

  -0.0107 - 0.0448i

  -0.0211         

Так как действительная часть корней характеристического уравнения отрицательная, то система устойчива.

  >> margin(Wz1)

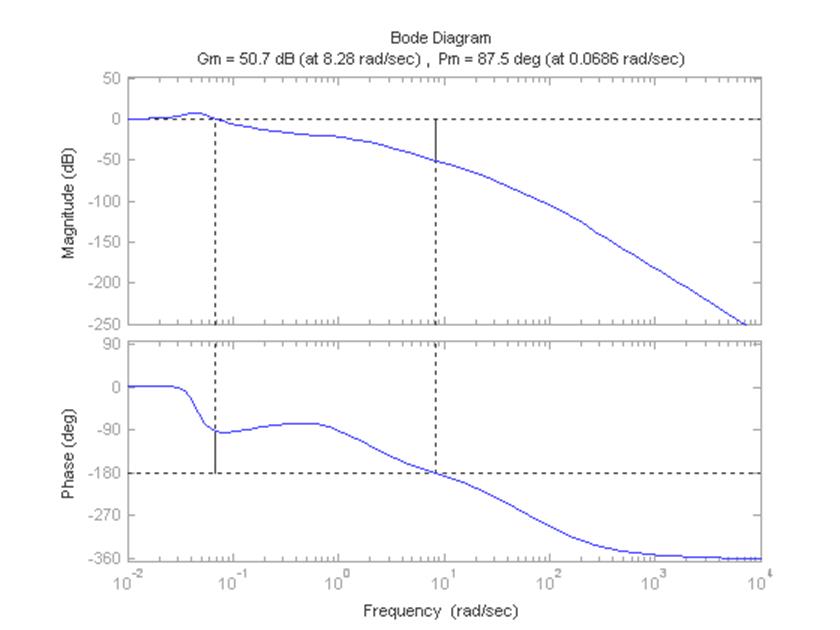
Рисунок 3 – Диаграмма Боде замкнутой САУ

Построение годографа Найквиста:

>> nyquist(Wz1)

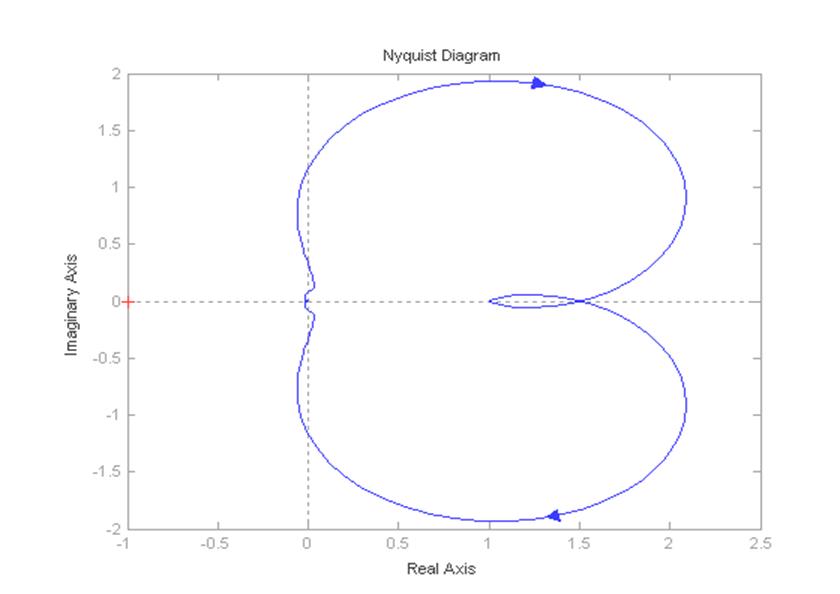
Рисунок 4 – Годограф Найквиста замкнутой САУ

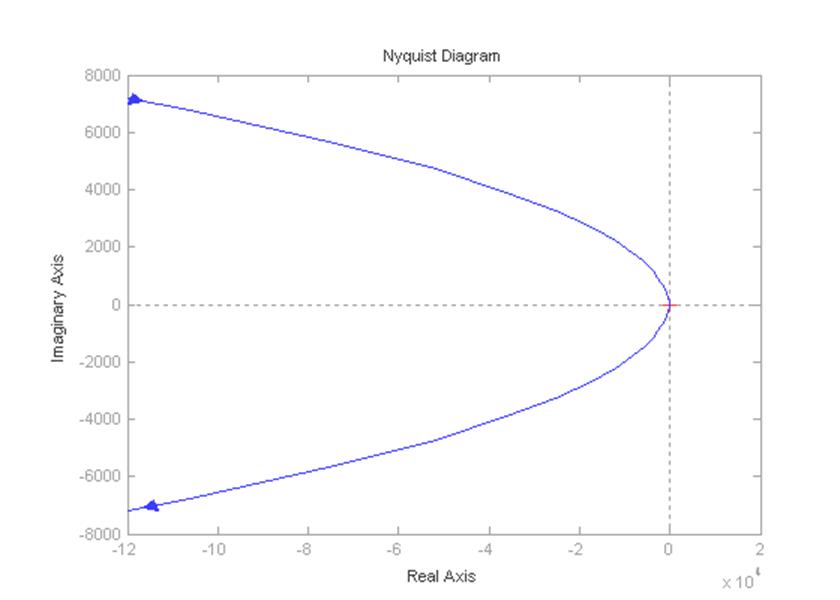
Рисунок 5 - Годограф Найквиста разомкнутой САУ

Кривая годографа охватывает действительную ось слева от ( – ∞, – 1) в бесконечности. Следовательно, данная система в замкнутом состоянии будет устойчива.

Построение переходной характеристики замкнутой САУ:

>> step(Wz1)