Исследование устойчивости линейных непрерывных систем автоматического управления. Вариант № 1, страница 2

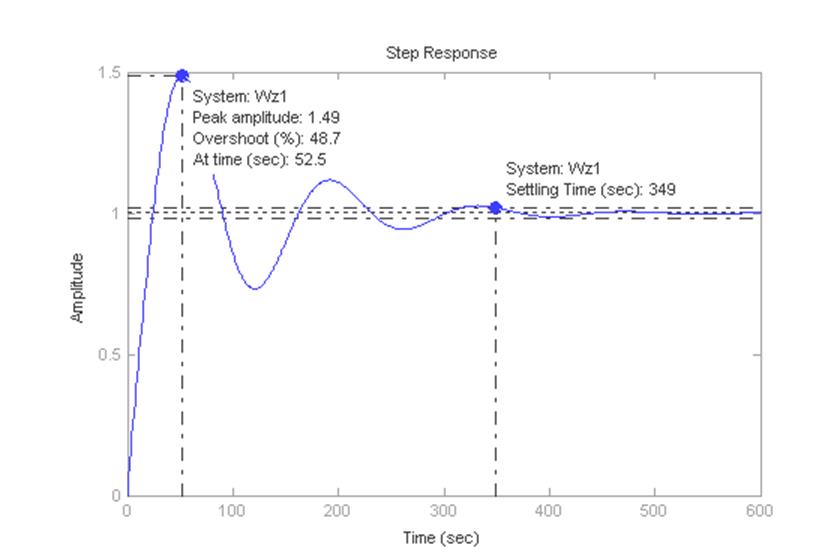
Рисунок 6 – Переходная характеристика замкнутой САУ

Максимальное перерегулирование для передаточной функции определится:

(1.49-1)/1*100%=49%

Время переходного процесса до входа в зону 0.05hуст  определится:

t=349с;

При k=kmax/3

>> W2=(5000/3)*W

Zero/pole/gain:

    120000 (s+0.03571)^2 (s+0.3472)

----------------------------------------

s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

>> Wz2=feedback(W2,1)

 Zero/pole/gain:

                      120000 (s+0.3472) (s+0.03571)^2

----------------------------------------------------------------------------

(s+99.79) (s+41.27) (s+0.3315) (s+0.039) (s+0.03318) (s^2  + 1.351s + 30.08)

>> tzero(Wz2)

ans =

   -0.3472

   -0.0357

   -0.0357

>> pole(Wz2)

ans =

 -99.7935         

 -41.2729         

  -0.6754 + 5.4432i

  -0.6754 - 5.4432i

  -0.3315         

  -0.0390         

  -0.0332     

Так как действительная часть корней характеристического уравнения отрицательная, то система устойчива.

>> margin(Wz2)

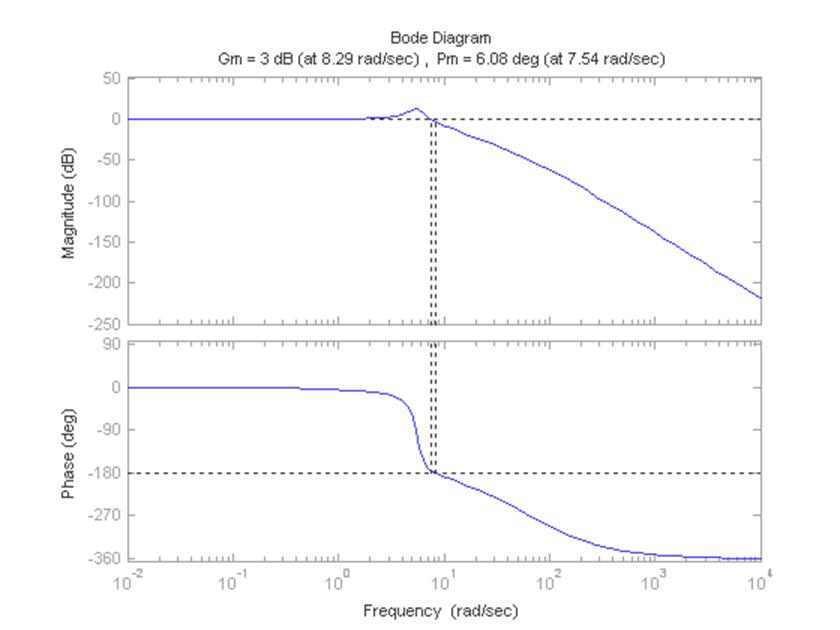
Рисунок 7 – Диаграмма Боде замкнутой САУ при k=kmax/3

Построение годографа Найквиста для замкнутой САУ при k=kmax/3

>> nyquist(Wz2)

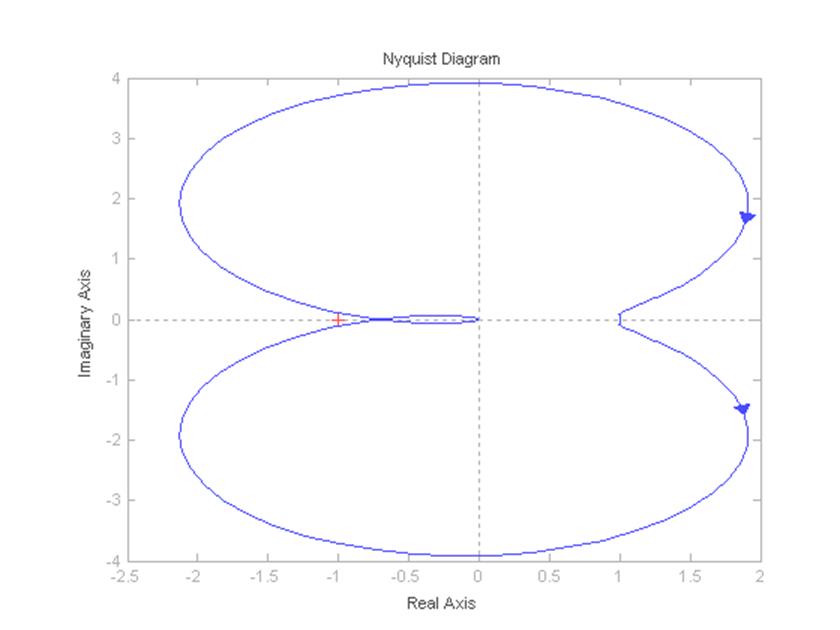
Рисунок 8 – Годограф Найквиста замкнутой САУ при k=kmax/3

Построение годографа Найквиста для разомкнутой САУ при k=kmax/3

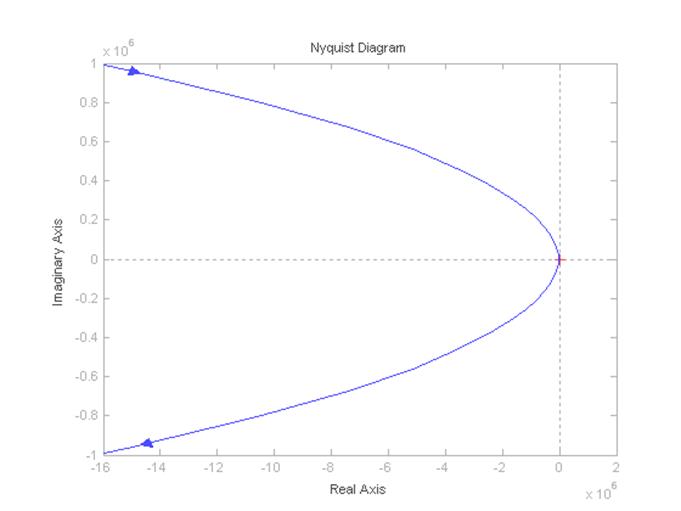
Рисунок 9 - Годограф Найквиста разомкнутой САУ

Построение переходной функции замкнутой САУ:

>> step(Wz2)

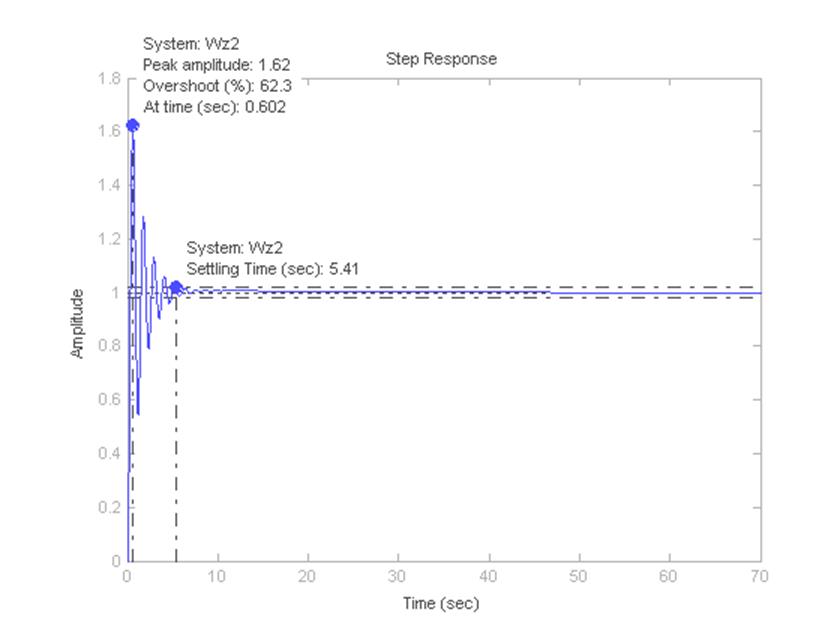
Рисунок 10 – Переходная характеристика замкнутой САУ при k=kmax/3

Максимальное перерегулирование для передаточной функции Wz2 определится:

(1.62-1)/1*100%=62%

Время переходного процесса до входа в зону 0.05hуст  определится:

t=5.41с;

4.)  Исследование системы с заданным запасом устойчивости.

Запас по модулю 10дБ, по фазе 5^о.

>> ltiview

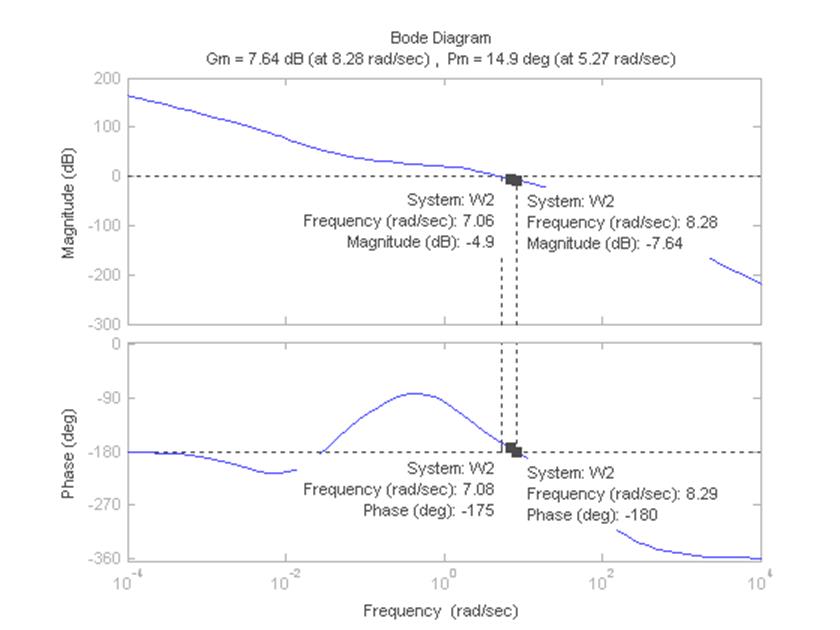
Рисунок 11 – Диаграмма Боде для W2

Определение коэффициентов, соответствующих заданным величинам запаса устойчивости по фазе и амплитуде:

Коэффициент, соответствующий заданному запасу по фазе определится:

 

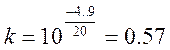
Коэффициент, соответствующий заданному запасу по амплитуде определится:

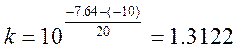
Определение передаточных функций систем с заданным запасом устойчивости по фазе и по амплитуде:

Определение передаточной функции системы с заданным запасом по фазе:

>> W3=W2/0.57

Zero/pole/gain:

  210526.3158 (s+0.03571)^2 (s+0.3472)

----------------------------------------

s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

 >> margin(W3)

Рисунок 12 – Диаграмма Боде для передаточной функции системы с заданным запасом по фазе

Определение передаточной функции системы с заданным запасом по амплитуде:

>> W4=W2/1.3122

 Zero/pole/gain:

91449.4742 (s+0.03571)^2 (s+0.3472)

    ----------------------------------------

s^2 (s+0.004) (s+1.408)^2 (s+40) (s+100)

 >> margin(W4)

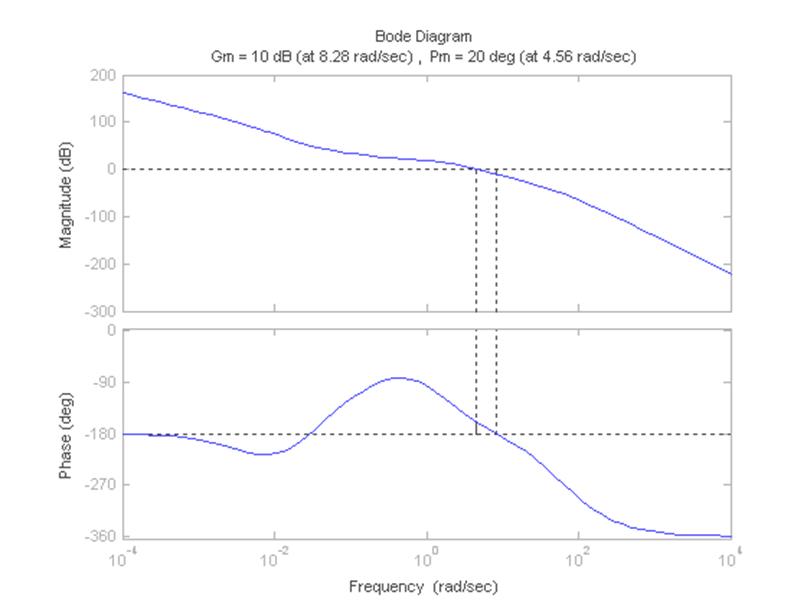
Рисунок 13 – Диаграмма Боде для передаточной функции системы с заданным запасом по амплитуде

>> ltiview

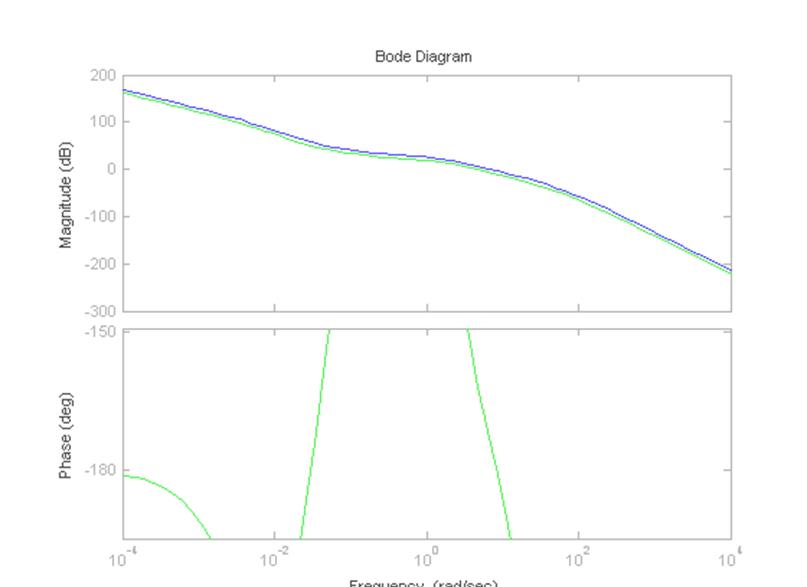
Рисунок 14 – Диаграммы Боде для двух передаточных функций

>> nyquist(W3,W4)

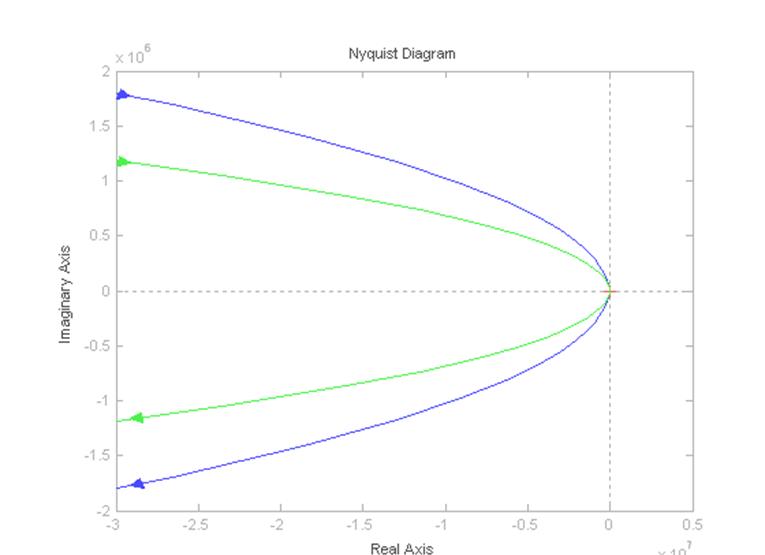
Рисунок 15 – Годографы Найквиста для функций W3, W4

вблизи точки (-1; j0)

Построение переходных характеристик для обеих передаточных функций Wz3, Wz4.

>> Wz3=feedback(W3,1)

Zero/pole/gain:

                     210526.3158 (s+0.3472) (s+0.03571)^2

------------------------------------------------------------------------------

(s+99.64) (s+42.17) (s+0.3382) (s+0.0381) (s+0.03375) (s^2  + 0.6056s + 51.02)

>> Wz4=feedback(W4,1)

Zero/pole/gain:

                     91449.4742 (s+0.3472) (s+0.03571)^2

------------------------------------------------------------------------------

(s+99.84) (s+40.98) (s+0.3266) (s+0.03956) (s+0.03285) (s^2  + 1.599s + 23.32)

>> step(Wz3,Wz4)

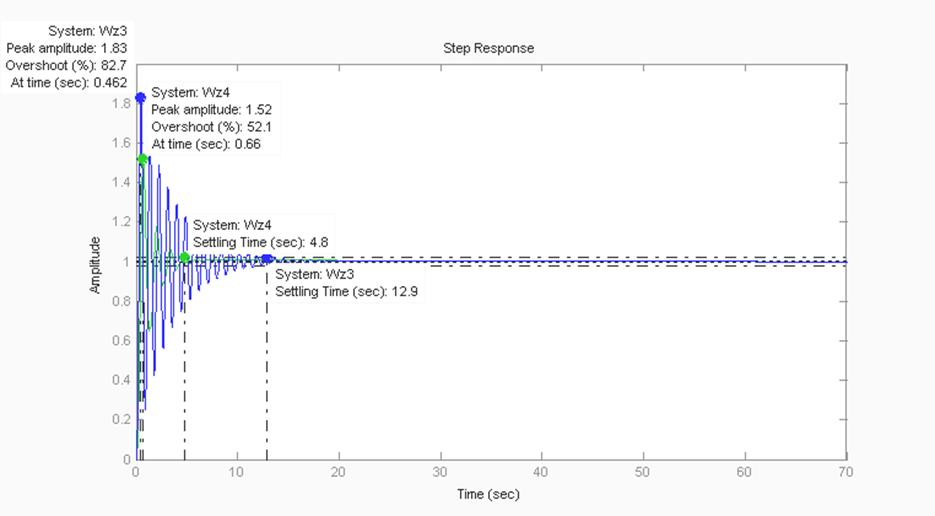
Рисунок 16 – Переходные характеристики для двух передаточных функций Wz3,Wz4.

Максимальное перерегулирование для передаточной функции Wz3 определится:

(1.83-1)/1*100%=83%

Время переходного процесса до входа в зону 0.05hуст  определится:

t= 12.9с

Максимальное перерегулирование для передаточной функции Wz4 определится:

(1.52-1)/1*100%=52%

Время переходного процесса до входа в зону 0.05hуст  определится:

t=4.8с