С другой стороны, при малых глубинах заложения можно допустить, что тепловой поток проходит только через слой грунта толщиной δr , находящийся над конструкцией канала. В этом случае получим расчетную зависимость, определяющую максимальную величину термического сопротивления грунта:
.
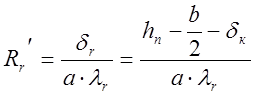(2)
Очевидно, расчеты с применением зависимости (2) дадут потери тепла с недостатком.
Таким образом, полагая Rr = 0, получим завышенные потери тепла qmax , а используя выражение (2) – заниженные qmin .
В действительности же 
, (3)
Следовательно, значение qmax и qmin дают верхнюю и нижнюю границы реальных линейных потерь тепла q: qmax > q > qmin , т.е., используя крайние значения Rr , определенные равенством (3), можно оценить действительные тепловые потери при малых глубинах заложения канала.
Полагая теперь, что термическое сопротивление грунта со стороны нижней и боковых стенок канала равноценно тепловому сопротивлению слоя над верхним перекрытием, получим окончательную расчетную формулу в виде:
.
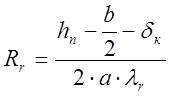(4)
|
|
|
|
|
|
0,9 1 1,1 1,2 1,3 1,4 1,5 |
- 0 0,0706 0,0991 0,1204 0,1380 0,1532 |
0,00367 0,0550 0,1063 0,1577 0,2090 0,2603 0,3117 |
0,00184 0,0275 0,0532 0,0788 0,1045 0,1302 0,1558 |
В таблице представлены
результаты расчета термических сопротивлений грунта по формулам (1), (2)
и (4) при малых глубинах заложения, когда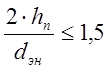 
λr = 1. Вычисления приведены для канала с размерами 
. Подобные же результаты получаются и при
иных габаритах конструкции.
Анализ приведенных
расчетных данных показывает следующее. При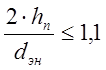 
термические
сопротивления, найденные по соотношению (1), резко падают, а при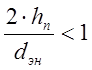 
расчет по этой формуле вообще невозможен.
В случае 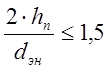значения Rr,
определенные на основе (1), подчиняются неравенству (3).
Величины Rr, вычисленные по уравнению (2), даны в третьей графе таблицы, а термические сопротивления грунта, рассчитанные с использованием зависимости (4), - в четвертой.
Сравнивая результаты второй
и четвертой граф расчетных данных, можно видеть, что по мере роста параметра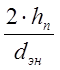 
значения Rr,
определенные по формулам (1) и (4), приближаются друг к другу.
Зависимость же (4) дает более надежные результаты при малых величинах
комплекса .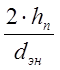
Таким образом, при малых
глубинах заложения канала, когда параметр 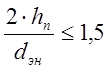расчет
термических сопротивлений грунта целесообразнее вести по формуле (4).
Падение температуры теплоносителя по длине трубопровода.
При движении теплоносителя по трубопроводам его температура падает. При транспортировке пара это приводит к выпадению конденсата.
В водяных тепловых сетях понижение температуры теплоносителя по длине трассы незначительно - 1ºС/1км пути. Причем, чем больше диаметр, тем меньше температура.
Как правило, разность температур в водяной тепловой сети не превышает 3-4% от значения температуры в начале тепловой сети. В этом случае расчет может быть проведен из условия постоянных удельных тепловых потерь. Уравнение теплового баланса в этом случае примет вид:
; 
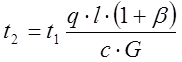, где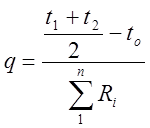 
Эта формула приближенная, решается методом последнего приближения.
Причем, при больших диаметров 
.
В паровых тепловых сетях,
транспортирующих насыщенный пар, температура пара определяется в каждой точке
на основе гидравлического расчета по падению давления 
.
При транспортировании
перегретого пара обычно известно Рн , Рк , tн, надо определить tк
. Для хорошо изолированных и непротяженных трубопроводов можно использовать
формулу: 
.
При плохо изолированных трубопроводах или их большой протяженности, когда разность температур значительно до 20-30ºС, необходимо в расчетах учитывать изменение удельных потерь q по длине трубопровода.
Термическое сопротивление изоляции паропровода – R
, знак
“-” т.к. температура понижается.
Или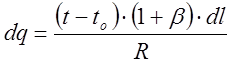 
; 
; 
;
; 
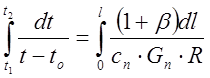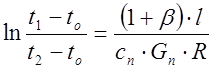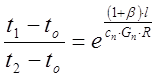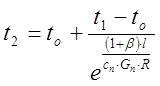
По этой формуле можно графически определить длину паропровода, где закончится перегрев пара.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
(1)
(2)