Системы теплоснабжения. Классификация систем теплоснабжения. Тепловое потребление. Совместная работа ТЭЦ и пиковых котельных. Определение стоимости (годовых затрат) перерасхода топлива, страница 29

1. Если у абонентов установлены регуляторы расхода РР, то известны расходы воды у абонентов (они постоянны) G_i и сопротивления участков магистралей сети S_i . Требуется определить G_i по магистралям ().
2. Если у абонентов не установлены РР, то известен напор Н_о в узле подвода сетевой воды к кольцу и сопротивления всех участков S_i . Требуется определить расход воды в системе и по участкам сети.

1. Расчет потокораспреления в кольцевой сети с РР у абонентов.

      Вода со станции поступает в узел 0 и распределяется по участкам I и IV магистрали между абонентами 1-3. Расходы воды у абонентов G₁, G₂, G₃ заданы и поддерживаются постоянными регуляторами расхода на вводах. Суммарный расход воды:

. Требуется определить G_I , G_II , G_III , G_IV .

Условимся, что:

а) приток воды в узел – “+”;

    отток воды из узла – “-“.

б) ΔН потока, протекающего по часовой стрелке – “+”;

    ΔН потока, протекающего против часовой стрелки – “-“.

Первый закон Кирхгофа: алгебраическая сумма расходов воды в любом узле равна нулю.

.

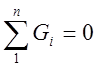Второй закон Кирхгофа: алгебраическая сумма потерь напора для любого замкнутого кольца равна нулю.

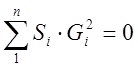
 Расчет производится методом последовательного приближения:

1. Задать произвольно распределение расходов воды по участкам, удовлетворяющим первому закону Кирхгофа  ;  ; .
2. По второму закону определяем невязку потерь напора в кольце

           

Если (положительно), то участки, в которых расход направлен по часовой стрелке – перегружены, а против часовой стрелки – недогружены.

3. Для увязки потерь напора вводят увязочный расход .

             должен вычитаться из предварительно выбранного расхода на перегруженных участках и добавляться на недогруженных.

 может быть определен из второго закона, если принять и ввести  в правую часть уравнения:

Решая это уравнение, и, пренебрегая членами, соединяющими , получим:

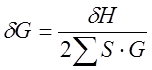 , где      

имеет тот же знак, что и .

4. Уточняют расходы на участках и вновь проводят проверочный расход по второму закону.

Обычно удовлетворительные результаты получают после второй поравки.

2. Расчет потокораспределения в кольцевой сети без РР.

      Расчет сводится к определению точки водораздела в кольце, удовлетворяющей второму закону Кирхгофа. Первое уравнение Кирхгофа не может быть использовано, т.к. расходы воды у абонентов  заранее не известны. Задача решается тоже методом последнего приближения.

1. Задать точку водораздела – точка 3.
2. Задать долю расхода φ, поступающего в точку 3 из III от G₃ . Доля расхода, поступающего из IV, будет соответственно равна 1 – φ.
3. Сопротивление систем:

    ;       определяется по правилам сложения сопротивлений для последовательных участков и проводимостей, а для параллельных участков – как для радиальных сетей с ответвлениями.

Т.к. в ответвление 3 поступает два потока воды из двух магистралей III и IV, то в соответствии с правилом, что при одновременном поступлении в систему нескольких потоков воды, каждый из потоков испытывает сопротивление, равное сопротивлению системы, деленному на квадрат долевого расхода данного потока, получим:

Поток из III →   ;

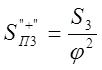Поток из IV → 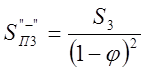   , где S₃ – сопротивление ответвления 3.

4. Расход воды в кольцевой сети:

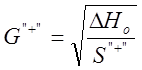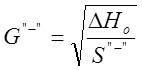;    , где ΔН_о – перепад в точке 0.

5. Определяют расход воды на всех участках сети по формуле:

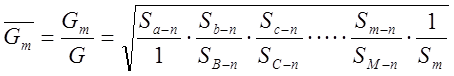
Проверяют выполнение условия:

6. Если невязка будет положительной, то уменьшают долю расхода из III магистрали φ или

 смещают точку водораздела в точку 2. При отрицательной невязке, соответственно, все наоборот.

7. Уточняют расчет до тех пор, пока не будет выполняться второй закон Кирхгофа.

3. Расчет потокораспределения в сети, питаемой от нескольких источников.

      В современных системах теплоснабжения обычно используют закольцованные сети от нескольких источников. Применение таких схем дает возможность повысить технико-экономические показатели по сравнению с обычными радиальными системами:

а) возможность перераспределения нагрузки между источниками;