Условие задачи 1.35(а)
В основе расчетных соотношений, которые будут удовлетворять условиям задачи, лежит математическая модель стационарной теплопроводности при граничных условиях III и I родов. Считаем тело однородным, изотропным; физические параметры постоянны; внутренние источники теплоты в теле отсутствуют.
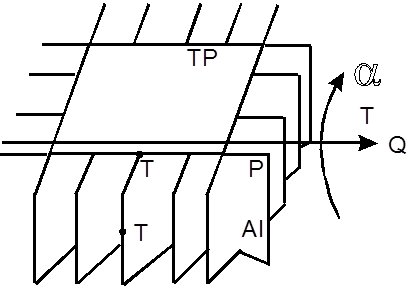 |
Коэффициент теплоотдачи a от поверхности радиатора к воздуху будем считать постоянным по всей поверхности. Также будем полагать, что теплопроводность алюминия, из которого сделан радиатор, достаточно велика (l®¥ ). Поперечное сечение очень мало по сравнению с длиной ребер - это дает основание пренебречь изменением температуры в поперечном сечении и считать, что она изменяется только вдоль оси стержня. Отсчет температуры будем вести от Тв=const.
Избыточная температура стержня:
V = Тр -Тв , (1) [1,стр. 49]
где Тв - температура воздуха, °С;
Тр - текущая температура радиатора, °С.
При граничных условиях III рода тепловой поток с поверхности радиатора:
Q = a VFE , (2) [1, стр. 53]
где a – коэффициент конвективной теплоотдачи, Вт/(м2× град);
F - общая площадь поверхности радиатора, м 2 ;
Е - эффективность ребра.
Е = 1 при l®¥
Из (2) имеем:
Q = a F(Тр-Тв)
Тр = (Q/ a F)+Тв , (3)
По условию задачи необходимо найти рабочую температуру транзистора. Для этого используем формулу для передачи теплоты через плоскую стенку при граничных условиях I рода, для которой тепловой поток выражается следующим образом:
Q = (Ттр-Тр)/R , (4) [1 стр.27]
где Ттр – температура транзистора, °С ;
R – контактное термическое сопротивление между корпусом транзистора и
радиатором, град/Вт;
Из (4) имеем:
Ттр = Q×R + Ттр , (5)
Q = 250 мВт = 250×10-3Вт ,
a = 12 Вт/(м2×град) ,
Тв = 25°С ,
lAl = 202 Вт/(м×град) , [2, стр.257]
R = 60 град/Вт .
Ттр - ?
Подставляем в (3):
Тр = 250×10-3/12×10×10-4 + 25 = 45,83 °С
Подставляем в (5):
Ттр = 250 ×10-3×60 + 45,83 = 60,83 °С
Условие задачи 4.35
Изолированная черная прямоугольная поверхность ориентирована перпендикулярно солнечным лучам. Космический корабль находится на расстоянии 1.5×108км от Солнца ; диаметр Солнце 1.39 ×106км. Принимаем, что Солнце – черное тело при температуре 5550 К, энергия излучения, падающая от других частей космического корабля и от планет, пренебрежительно мала. Окружающее пространство имеет эквивалентную радиационную температуру 0 К. Рассчитать равновесную температуру черной поверхности.
 e1 = 1
e1 = 1
1 Т1
![]()


![]() w
w
![]()
Трад = 0 К
2 - r
 |
![]()
![]() e2 = 1
e2 = 1
![]()
![]() Т2
Т2
В основе расчетных соотношений, которые будут удовлетворять условиям задачи, лежит математическая модель равновесного излучения между двумя черными телами, произвольно расположенными в пространстве, а также свойство взаимности лучистых потоков.
![]()
![]() Рассмотрим два черных тела (корабль и Солнце), находящихся в
пространстве с эквивалентной радиационной температурой Трад. Допустим, что тела
имеют изотермические поверхности с температурами Т1 и Т2.
Самооблучение их отсутствует (j1,1 = j2,2 = 0). Теплообмен этих тел с другими телами также
отсутствует. Тела являются однородными, изотропными: яркость излучения не
зависит от направления. Так как тела черные, то e1 = e2 = 1).
Рассмотрим два черных тела (корабль и Солнце), находящихся в
пространстве с эквивалентной радиационной температурой Трад. Допустим, что тела
имеют изотермические поверхности с температурами Т1 и Т2.
Самооблучение их отсутствует (j1,1 = j2,2 = 0). Теплообмен этих тел с другими телами также
отсутствует. Тела являются однородными, изотропными: яркость излучения не
зависит от направления. Так как тела черные, то e1 = e2 = 1).
На каждом из рассматриваемых тел выделим элементарные площадки dF1 и dF2, бесконечно малые по сравнению с расстоянием r между их центрами.
Из условия равновесного излучения плотность потока результирующего излучения Ерез = 0.
Ерез = Есоб01 - Епад01 , [1, стр. 397]
отсюда
Епад1 = Есоб01 , (1)
где Епад1 – плотность потока падающего излучения на тело 1, Вт/м2;
Есоб01 – плотность потока собственного излучения черного тела 1, Вт/м2;
По закону Стефана – Больцмана:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.