Есоб01 = s0 Т14 , (2) [1, стр. 372]
где s0 – постоянная Стефана – Больцмана, Вт/м2×К4;
Т1 – термодинамическая температура тела 1, К.
Аналогично:
Есоб02 = s0 Т24 , (3) [1, стр. 372]
где Т2 – термодинамическая температура тела 2, К
Плотность падающего солнечного лучистого потока определяем следующим образом:
Епад = В×w , (4) [2, стр. 184]
где В – яркость солнечного излучения, Вт/м2×стер;
w - телесный угол, под которым единичная площадка “видит” Солнце.
В = Есоб01/ p = s0 Т1/ p , (5) [2, стр. 184]
w = p× d/4×r2 , (6) [2, стр. 185]
где d – диаметр Солнца, м;
r – расстояние между телами, м.
Подставляя выражение (5) и (6) в (4), получаем:
Епад = s0× Т14×d2/ 4×r2 = s0× Т24
Отсюда, выражая неизвестную температуру Т2, находим равновесную температуру изолированной черной поверхности космического корабля:
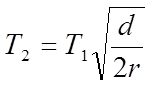, (8)
r = 1,5×108км,
d = 1,39×106км,
Т1 = 5550 К,
Трад = 0 К.
Т2 - ?
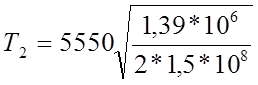= 377,7 К = 104,7°С
Ответ : Т2 = 104,7°С
Условие задачи 2.35
Рассчитать скорость испарения воды с поверхности озера, имеющего размеры приблизительно 500х500 м. Скорость ветра 5м/с. Температура воздуха и воды в озере равна 25°С. Рассчитать скорость испарения воды для случаев, когда окружающий воздух имеет относительную влажность а) 10%, б)80%.
 |
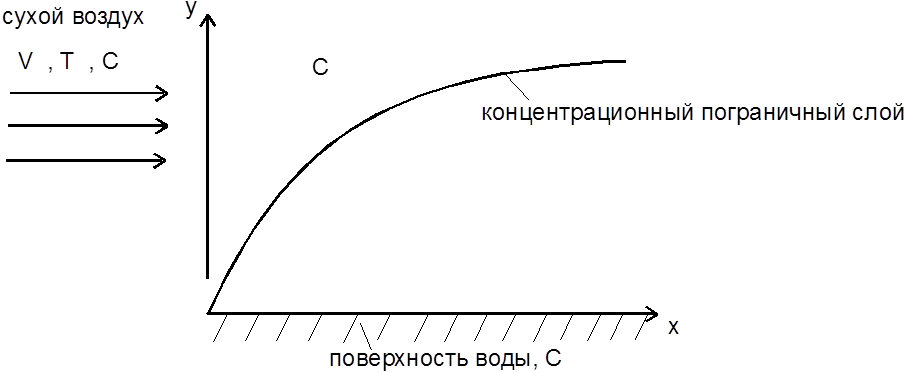В основе расчетных соотношений, которые будут удовлетворять условиям задачи, лежит математическая модель процесса массообмена при вынужденной конвекции от плоской пластины (граничные условия III рода).
Задача испарения воды из озера подобна задаче о переносе тепла от горизонтальной плоской пластины, на поверхности которой развивается тепловой пограничный слой. Аналогичным образом образуется концентрационный слой, внутри которого концентрация изменяется в направлении, перпендикулярном горизонтальной поверхности озера.
Снаружи пограничного слоя концентрация водяного пара остается постоянной и равной своему значению в окружающей среде.
Эта задача иллюстрирует подобие между процессами конвективного теплообмена и массообмена, где температура Т подобна массовой концентрации СА, коэффициент температуропроводности а подобен коэффициенту диффузии ДАВ.
Число Нуссельта: Nu = a×L/ lср [1, стр. 153]
подобно числу Шервуда: Sh = hm × L/ ДАВ , (1) [2, стр. 465]
где a - коэффициент теплоотдачи, Вт/(м2×К) ;
L – характерный размер, м ;
lср – теплопроводность среды, Вт/(м×К);
hm – коэффициент конвективного массообмена, м/с ;
ДАВ – коэффициент диффузии, м2/с.
Число Прандтля: Pr = n/а [1, стр. 155]
подобно числу Шмидта: Sc = n/ДАВ , (2) [5, стр. 465]
где n - кинематическая вязкость, м2/с;
а – коэффициент температуропроводности, м2/с.
Данная задача рассматривает гетерогенную систему воздух – вода. Поверхность жидкой фазы играет роль, аналогичную роли твердой стенки в процессах теплоотдачи без сопутствующей диффузии. Тепло- и массообмен идут одновременно.
Допустим, что отсутствуют возбудители движения, посторонние для рассматриваемого процесса испарения. Будем полагать, что полное давление по всему объему парогазовой смеси неизменно, а температурные разности пренебрежимо малы. Концентрация пара изменяется от значения САs на поверхности испаряющейся жидкости до значения СА¥ вдали от поверхности раздела.
Прежде чем подобрать безразмерное соотношение для числа Шервуда, следует определить, будет ли течение ламинарным или турбулентным.
Физические параметры воздуха при температуре t = 25°С:
r = 1,146 кг/м3, m = 18,46×10-6Н×с/м2, n = 16,18×10-6м2/с, Рнас = 3098Н/м2.
Число Рейнольдса равно: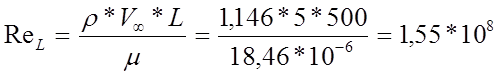 
, (3) [1,
стр. 153]
ReL > Reкр = 5×105 , [3, стр. 65] Þ течение воздуха турбулентное
где r - плотность воздуха, кг/м3;
V¥ - скорость набегающего потока, м/с ;
m - динамическая вязкость, Н × с/м»;
Рнас – давление насыщения, Н/м2.
Так как течение воздуха турбулентное, то соответствующее безразмерное соотношение аналогично соотношению для конвективного теплообмена:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.