Министерство общего и профессионального образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра тепловых электрических станций
Факультет: ФЭН
Студент: Русских Е.
Преподаватель: Саломатов В.В
Вариант: 7
Отметка о защите:
НОВОСИБИРСК 1999
Условие задачи: Колба медицинского термометра имеет диаметр 7мм и длину 10мм. Термометр вынимают из спиртового раствора и помещают его в рот пациента. Вследствие испарения спиртового раствора начальная температура термометра 18°С. Найти минимальное время по истечении которого медсестра должна вынуть термометр, причем его показание не должно отличаться от истинной температуры более чем на 0,5°С. Теплофизические свойства колбы термометра можно приближенно принять равными средним значениям между свойствами ртути и стекла, Найти требуемое время при трех значениях среднего коэффициента конвективной теплоотдачи к колбе термометра:a= 10;50 и 100 Вт/(м2*К)
Решение:
В основе расчетных соотношений удовлетворяющих условиям поставленной задачи, положена математическая модель нестационарной теплопроводности при граничных условиях третьего рода.
Расчетно – числовые соотношения получены из следующих допущений:
1. Тело однородно.
2. Тело изотропно.
3. Теплофизические свойства постоянны.
4. Внутренние источники теплоты отсутствуют.
Теплофизические параметры ртути и стекла колбы, согласно рекомендациям задачи следующие [1,стр.470]:
|
Ртуть |
Стекло |
Среднее |
|
|
а, м2/с |
4,25*10-6 |
0,445*10-6 |
0,35*10-6 |
|
l, Вт/(м*°С) |
0,745 |
4,9 |
2,82 |
|
С, кДж/(кг°С) |
0,139 |
0,67 |
0,4 |
|
r, кг/м3 |
13550 |
2590 |
8070 |
Рассчитаем значение числа Био при различных значениях коэффициента теплоотдачи a:
а) a=10
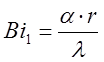 (1) [2,стр. 226]
(1) [2,стр. 226]
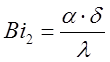 (2) [1,стр. 53]
(2) [1,стр. 53]
где r – радиус цилиндра, м;
d - половина длины цилиндра, м;
l - теплопроводность материала цилиндра, Вт/(м*°С);
a - коэффициент теплоотдачи, Вт/(м2*К);
Подставляя исходные данные определим числа Био:
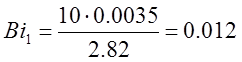
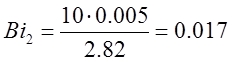
б) a=50
Подставляя исходные данные в формулы (1) и (2) получим:
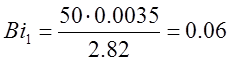
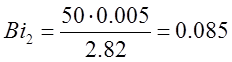
в) a=100
Подставляя исходные данные в формулы (1) и (2) получим:
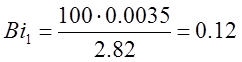
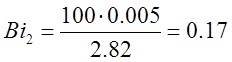
Так как значения чисел Био малы, колба может быть отнесена к термически тонкому телу.
Составим баланс:
dQакк= dQконв (3)
где dQакк – теплота, аккумулирующаяся в теле.
dQконв – теплота, принятая телом в процессе конвективного теплообмена.
dQконв=a*F*J*dt (4)
где a - коэффициент теплоотдачи, Вт/(м2*К);
F – площадь поверхности, м2;
J - избыточная температура, °С;
J=tc-tв (5) [1,стр. 49]
где tс – текущая температура тела, °С;
tв – температура окружающей среды, °С;
dQакк=С*r*V*dJ (6)
где С – теплоемкость, кДж/(кг°С);
r - плотность, кг/м3;
V – объем тела, м3;
Подставляя найденные члены в уравнение баланса (3), решим дифференциальное уравнение:
a*F*J*dt=С*r*V*dJ
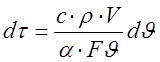
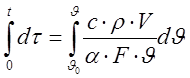
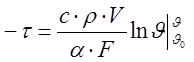
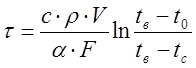 (7)
(7)
где tс –температура тела в момент времени t, °С;
t0 –температура тела в начальный момент времени, °С;
Проверка размерности формулы (7)
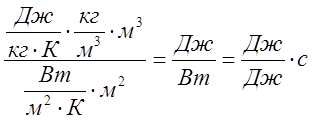 =
[c];
=
[c];
Считая что основную массу колбы термометра составляет ртуть примем среднюю плотность колбы равной плотности ртути.
Подставляя все известные величины в формулу (1) получим:
а) При a=10 Вт/(м2*К)
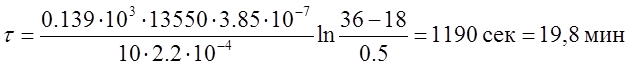
б) При a=50 Вт/(м2*К)
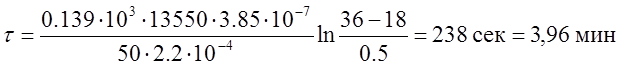
в) При a=100 Вт/(м2*К)
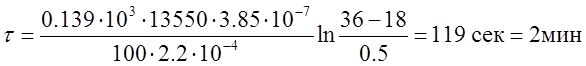
Погрешность вычисления (по сравнению с ответом)=2%
Условие задачи:
Тонкая константановая лента сечением 0,1*5 мм нагревается электрическим током силой I=20 А. Электрическое сопротивление 1 м ленты RL=1 Ом/м.
Лента обтекается продольным потоком воды. Скорость и температура набегающего потока w0=0,5 м/с; t0=10°C.
Определить температуру ленты на расстоянии 25 и 200 мм от передней кромки.
 |
Решение задачи.
В основе расчетных соотношений для данной задачи лежит математическая модель теплоотдачи при вынужденном продольном обмывании плоской поверхности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.