Расчет требуемого времени при трех значениях среднего коэффициента конвективной теплоотдачи к колбе термометра, страница 2

В ходе решения приняты следующие допущения:

1.  Течение и теплообмен стационарны.

2.  Скорость и температура за пределами гидродинамического и теплового пограничных слоев равны соответственно w₀ и t₀ .

3.  Внутренние источники теплоты в жидкости отсутствуют.

4.  Нет потерь на трение и диссипацию (так как скорость набегающего потока много меньше скорости звука).

5.  Теплоотдачей с торцов пластины можно пренебречь.

Таблица теплофизических свойств воды при температуре t₀=10°C:

t0, °С	l, Вт/(м*°С)	а, м2/c	n, м2/с
10	0,574	13,7*10-8	1,306*10-6

 Здесь и в дальнейшем теплофизические свойства воды  взяты из [2, стр.260]

Составим баланс:

Q_подв=Q_конв ,                               (1)

 где Q_подв -теплота подводимая к системе за счет внутреннего источника тепла в пластине.

Q_конв –теплота, отводимая от пластины в процессе конвективного теплообмена

Согласно закону Ньютона – Рихмана , тепловой поток Q_конв при теплоотдаче:

Q_конв=aF(t_c-t_ж) , [1, стр.126]     (2)

 где a-коэффициент теплоотдачи , Вт/(м²*К);

        t_c -температура пластины на расстоянии х , К;

        t_ж -температура воды , К;

        F –площадь поверхности пластины ,м² ;

Согласно закону Джоуля-Ленца:

Q_подв=I²*R ,                                 (3)

 где I-сила тока , А;

       R-электрическое сопротивление материала пластины, Ом;

Подставляя значения Q_подв и Q_конв в формулу (1), получим:

aF(t_c-t_ж)= I²*R                              (4)

Из формулы (4) получаем:

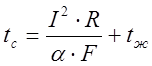                            (5)

Дальнейшее решение данной задачи сводится к определению коэффициента теплоотдачи a  в каждом конкретном случае.

а) х=0,025 м

Рассчитаем значение числа Рейнольдса на длине х=0,025 м

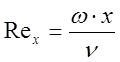  , [1, стр.153 ]                                  (6)

  где w - скорость потока, м/с;

        х – характерый размер, м;

         n - кинематическая вязкость, м²/с;

Подставив  данные в формулу (6),получим:

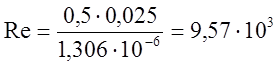<10⁵

Так как значение Re меньше критического значения числа Рейнольдса Re_kp=10⁵ ,

то режим течения ламинарный. [1, стр.153]

Исходя из выбранной математической модели, учитывая что q_ст=const,  определим значение числа Нуссельта:

                       (7)    [1, стр.188]

 где х₀ – длина начального необогреваемого участка, м;

       х₁ – координата отсчитываемая от начала обогреваемого участка, м;

       Re_x – значение числа Рейнольдса на длине х₁;

        Pr_ж - значение числа Прандтля при температуре t₀;

        e - коэффициент, учитывающий неизотермичность пластины;

       Pr_ж/ Pr_с –поправка, учитывающая изменение физических параметров жидкости;

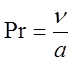                                                            (8)   [1, стр. 155]

  где n - кинематическая вязкость, м²/с

         а –температуропроводность, м²/с

Рассчитаем значение числа Прандтля  :

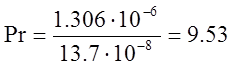
Так как в данной задаче необогреваемый участок отсутствует, безразмерный комплекс (x₁/x)^0.2=1

Согласно рекомендациям  [1, стр.188] при q_ст=const,  коэффициент e=1,36

Так как температура стенки неизвестна, задачу решаем методом последовательных приближений.

Принимаем t_c=35°C

Подставив исходные данные в формулу (7) рассчитаем значение числа Нуссельта:

Исходя из определения:

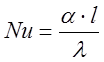                                                    (9)   [1, стр. 153]

  где a-коэффициент теплоотдачи, Вт/(м²*К);

        l – характерный линейный размер ,м;

        l - теплопроводность жидкости, Вт/(м*°С);

Выражая из формулы (9) значение коэффициента теплоотдачи получаем:

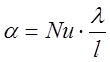              (10)

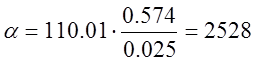 Вт/(м²*К)

Подставляя полученные значения в формулу (5) получаем:

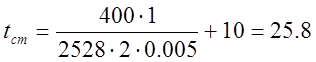°С