Расчет требуемого времени при трех значениях среднего коэффициента конвективной теплоотдачи к колбе термометра, страница 3

Так как рассчитанная температура t_ст сильно отличается то принятой, делаем второе приближение

Принимаем t_c=27°C

Подставив исходные данные в формулу (7) рассчитаем значение числа Нуссельта:

Определим  значение коэффициента теплоотдачи :

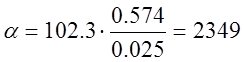 Вт/(м²*К)

Подставляя полученные значения в формулу (5) получаем:

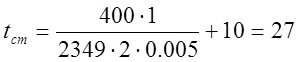°С

Расчетная и заданные температуры сошлись, и третьего приближения не требуется.

б) х=0,02 м

Рассчитаем значение числа Рейнольдса на длине х=0,02 м

Подставив исходные данные в формулу (6) получим:

    

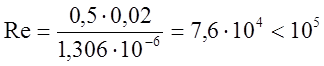
Так как значение Re меньше критического значения числа Рейнольдса Re_kp=10⁵ ,

то режим течения ламинарный. [1, стр.153]

Принимаем t_c=80°C

Подставив исходные данные в формулу (7) рассчитаем значение числа Нуссельта:

Рассчитаем значение коэффициента теплоотдачи по формуле (10):

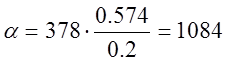 Вт/(м²*К)

Подставляя полученные значения в формулу (5) получаем:

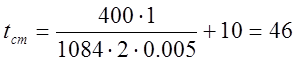°С

Так как рассчитанная температура t_ст сильно отличается то принятой, делаем второе приближение

Принимаем t_c=51°C

Подставив исходные данные в формулу (7) рассчитаем значение числа Нуссельта:

Определим  значение коэффициента теплоотдачи :

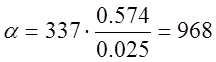 Вт/(м²*К)

Подставляя полученные значения в формулу (5) получаем:

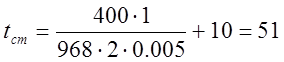°С

Расчетная и заданные температуры сошлись, и третьего приближения не требуется.

Ответ:     При х=25 мм                    t_ст=27°С

                При х=200 мм                  t_ст=51°С

Условие задачи:

Определить коэффициент теплоотдачи и температуру внутренней поверхности трубы при кипении воды в трубе диаметром d=38 мм, если плотность теплового потока q=2*10⁵ Вт/(м²*К), скорость и давление воды w=1 м/с, р=2,8 МПа.

Решение:

В основе расчетных соотношений для данной задачи лежит математическая модель теплообмена при кипении однокомпонентных жидкостей.

Допущения при решении задачи:

1. Происходит кипение жидкости в условиях вынужденной конвекции.

2. Течение и теплообмен стационарны.

3. Внутренние источники теплоты в жидкости отсутствуют.

4. Тепловой поток от поверхности нагрева воспринимается жидкой фазой.

5. Размеры поверхности нагрева велики по сравнению с размерами паровых пузырьков.

6. Теплофизические свойства постоянны.

7. Влиянием сил тяжести можно пренебречь.

При вынужденном движении кипящей жидкости в трубах в условиях, когда жидкость нагрета до температуры насыщения, коэффициент теплоотдачи может быть посчитан по следующим  формулам [2, стр. 177]:

  при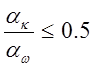     a=a_w;                                    (1)

 при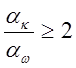         a=a_k;                                    (2)

 при 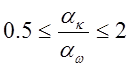 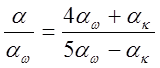                 (3)

 где a- коэффициент теплоотдачи при вынужденном движении кипящей жидкости в трубах, Вт/(м²*К);

      a_k- коэффициент теплоотдачи при развитом пузырьковом кипении в большом объеме, Вт/(м²*К);

      a_w- коэффициент теплоотдачи при турбулентном движении однофазной жидкости в трубах, Вт/(м²*К);

Определим значение коэффициента теплоотдачи при движении однофазной жидкости a_w:

При р=2,8 МПа  t_s=230 °C ; n_ж=0.145*10^-6 м²/с ; l_ж=0,637 Вт/(м*°С) ; Pr_ж=0,88

 Здесь и в дальнейшем теплофизические свойства взяты из [1, стр. 468]

Решаем задачу методом последовательных приближений.

Так как  температура стенки неизвестна, условно примем ее равной t_ст=237 °С

При t_ст=237 °С   Pr_ст=0,87

Рассчитаем значение числа Рейнольдса

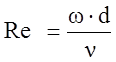  , [1, стр. 153]                                  (4)

  где w - скорость потока, м/с

        х – характерый размер, м

         n - кинематическая вязкость, м²/с

Подставляя данные находим:

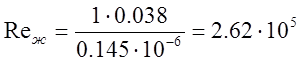 -режим движения турбулентный

С учетом  рекомендаций [1, стр. 215] для теплоотдачи при турбулентном режиме течения рассчитаем значение числа Нуссельта: