Составление простейшей электрической системы («электропередачи»), страница 7

по отклонению параметра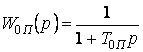                    

по производной отклонения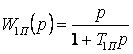                

для общего канала регулирования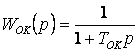       

где  – параметры режима

С учётом исходных данных варианта запишем значение напряжения на выходе регулятора:

 DE_r = (KW_OK                                                                                                (4.7.1)

W_OK = 1     W=1       W= p

=2(4.7.2)

 

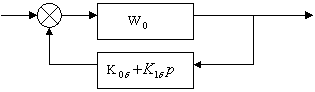
Рисунок 4.7.1

 где W-ПФ разомкнутой системы

4.8Составить характеристический определитель (ХО), характеристический полином (ХП) и передаточные функции (ПФ) параметров регулирования замкнутой системы: . Определить корни ХП при заданных значениях коэффициентов регулятора

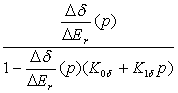⁼                                     (4.8.1)

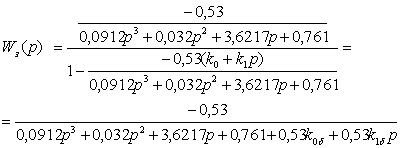                                       (4.8.2)

При заданных значениях коэффициентов регулятора (K=1 и K) ПФ примет вид:

                                                                         (4.8.3)

Характеристический полином замкнутой системы:

D(p)=                                              (4.8.4)

Используя программу корни, найдем корни полинома:

р₁= -0,311041617133472

p -0,019917787924492  - j6,7461277097

p= -0,019917787924492  + j6,7461277097

Т.к. вещественные части всех корней отрицательны, то система в замкнутом состоянии статически устойчива.

4.9Рассчитать аналитически особые точки (для нулевой и резонансной частоты) ЧХ замкнутой системы и кривой Д-разбиения (области устойчивости). Варьируя коэффициенты ,  относительно граничных значений, показать достоверность построенной области устойчивости

Перейдём к частотной форме, применив преобразование Фурье:

p  à  jw

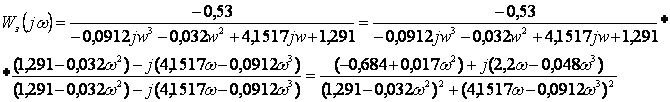Re(                                                  (4.9.1)

Im(                                   (4.9.2)

A()= 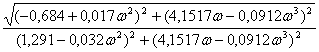                              (4.9.3)

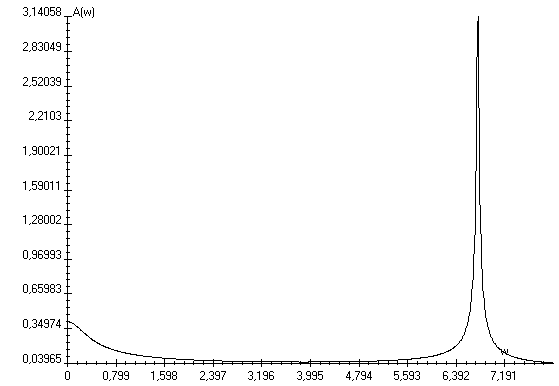
При  A(0)=0,41

При =6,749  A(6,749)=3,276

АЧХ и ФЧХ замкнутой системы: