4.3 Построить угловую характеристику активной мощности и определить коэффициент запаса апериодической устойчивости
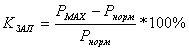
P
=
=
=1,65 (4.3.1)
P
=
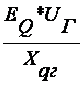*sindг =
*0,37=0,903(4.3.2)
K
=
*100%=83,33% (4.3.3)
|
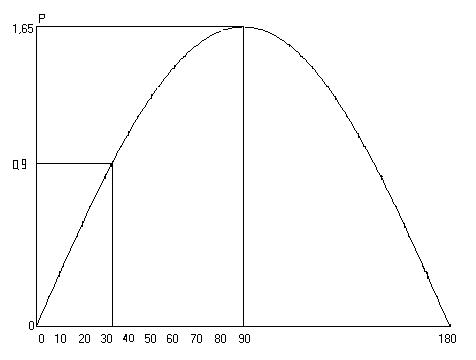
Рисунок 4.3.1 - Угловая характеристика мощности |
4.4 Составить дифференциальные уравнения движения Горева-Парка для электромеханических процессов и линеаризовать их в точке рассчитанного режима
Не учитывая демпферные контуры и исключая составляющие, обусловленные быстрозатухающими переходными процессами и изменением скорости вращения ротора относительно синхронной оси, запишем уравнения Горева-Парка в виде:
.
(4.4.1)
. (4.4.2)
.
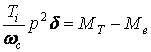(4.4.3)
.
(4.4.4)
Линеаризованные уравнения переходных процессов электропередачи, работающей на мощную приемную систему запишутся в виде:
.
(4.4.5)
.
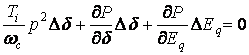(4.4.6)
,
(4.4.7)
где 
В полученных трёх уравнениях для исследования
статической устойчивости необходимо оставить коэффициенты только при двух
переменных: 
и 
.
Исключаем переменные 
и
посредством замены:
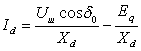и 
(4.4.8)
После некоторых преобразований от трёх уравнений переходим к системе двух линеаризованных уравнений с двумя неизвестными:
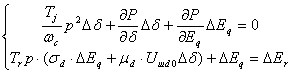(4.4.9)
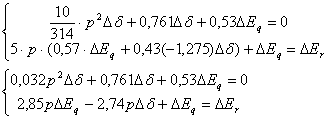(4.4.10)
4.5 Рассчитать аналитически частные производные по параметрам регулирования: ¶P/¶d, ¶P/ ¶Eq, ¶U/¶d, ¶U/ ¶Eq, ¶wu/¶pd , ¶wu/¶pEq
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.