![]()
 (4.5.1)
(4.5.1)
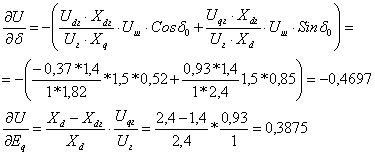 (4.5.2)
(4.5.2)
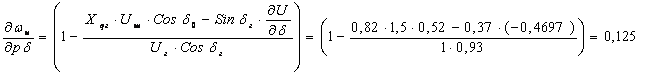
![]() (4.5.3)
(4.5.3)
4.6Используя значения частных производных, составить характеристический определитель (ХО), характеристический полином (ХП), и передаточные функции (ПФ) параметров регулирования разомкнутой системы: Dd/DEr , DEq/DEr . Определить корни характеристического полинома. Сделать выводы по статической устойчивости системы.
Используя частотные характеристики системы, рассчитать две особые точки ЧХ на «нулевой» и «резонансной» частотах
Составим характеристический определитель:
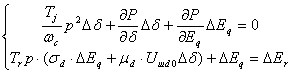 (4.6.1)
(4.6.1)
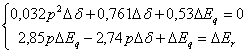 (4.6.2)
(4.6.2)
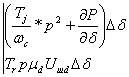
![]()
 =
=![]() (4.6.3)
(4.6.3)
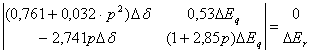 (4.6.4)
(4.6.4)
Обозначим:
![]() =0,761+0,032p
=0,761+0,032p![]()
![]() =-2,741p
(4.6.5)
=-2,741p
(4.6.5)
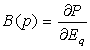 =0,53
=0,53
![]() =1+2,85p
(4.6.6)
=1+2,85p
(4.6.6)
Характеристический полином:
D=A*F-C*B=0,0912p![]() +0,032p
+0,032p![]() +3,6217p+0,761=0 (4.6.7)
+3,6217p+0,761=0 (4.6.7)
Передаточные функции параметров регулирования системы.
Передаточная функция по параметру ![]() :
:
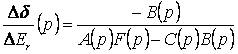 =
=![]() (4.6.8)
(4.6.8)
Передаточная функция по параметру ![]() :
:
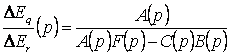 =
=![]() (4.6.9)
(4.6.9)
С помощью программы «КОРНИ» определяем корни характеристического полинома:
p![]() = -0,210278868500825
= -0,210278868500825
p![]() = -0,0702991622408157 + j6,29897737559206
= -0,0702991622408157 + j6,29897737559206
p![]() =
-0,0702991622408157 - j6,29897737559206
=
-0,0702991622408157 - j6,29897737559206
Разомкнутая система статически устойчива, т.к. вещественные части корней отрицательны.
Расчёт особых точек ЧХ на нулевой и резонансной частотах.
Получим выражение для АЧХ в виде:
А(![]() )=
)=![]() (4.6.10)
(4.6.10)
Перейдём к частотной форме, применив преобразование Фурье:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.