



Контрольные для ФБ
Первый семестр
Контрольная работа 1
Введение в анализ
1.
Записать
на языке ![]() определение
определение
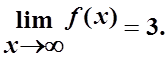
2. Доказать непрерывность функции y=sinx.
3.
Вычислить
а) 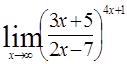 б)
б)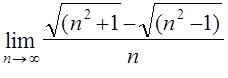
в)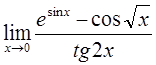 г)
г) 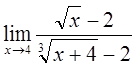
![]()
4.
Сравнить
бмф arcsin![]() и
и ![]()
![]()
![]() при
при ![]() .
.
5. Исследовать на непрерывность, сделать чертеж.
a)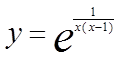 ,
б)y=
,
б)y=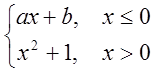
6. Построить графики функций.
a)![]() , б) y
= - |x-1| , в) r =
, б) y
= - |x-1| , в) r = ![]() .
.
Вариант для защиты ТР по теме «Дифференциальное исчисление функций одного переменного»
1.
Вычислить производные функций а) ![]() , в)
, в)![]() .
.
2.
Вычислить 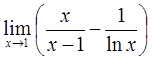 ,
используя правило Лопиталя.
,
используя правило Лопиталя.
3.
Составить уравнения касательной и
нормали к кривой ![]() в точке
в точке ![]() =p/6.
=p/6.
4.
Вычислить приближенно с помощью
дифференциала f(0,01) ,
если ![]() .
.
5.
Найти наибольшее и наименьшее
значения функции ![]() на отрезке [-4;2 ].
на отрезке [-4;2 ].
6.
Найти асимптоты и построить график
функции 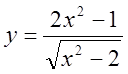 .
.
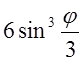 , 0 £j£p/4 .
, 0 £j£p/4 . 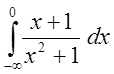 .
.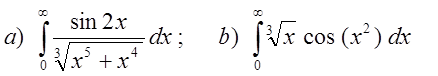 .
.Второй семестр
Контрольная работа по теме “Функции многих переменных”
1. Найти grad z(M0) и
производную ![]() в точке M0(1,1), по направлению l,
составляющему 60 градусов с осью ОX , если 3xyz =
y2 + z2+ x2.
в точке M0(1,1), по направлению l,
составляющему 60 градусов с осью ОX , если 3xyz =
y2 + z2+ x2.
2. На поверхности, заданной уравнением: x2 + y2 - z2 - 2x = 0 найти точки, где касательная плоскость параллельна плоскости y=0.
3. u=tg(3x-2y-z), M(p,p,3p/4). Вычислить du|M .
4. Исследовать функцию z = 3x2 + 2y2 - x3+ 4y на экстремум .
5. Найти область определения
функции z =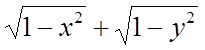 ,
изобразить область определения на плоскости ХОУ .
,
изобразить область определения на плоскости ХОУ .
6. Найти производные ![]() ,
, ![]() в точке
M0(p/3,1) от сложной функции
в точке
M0(p/3,1) от сложной функции
z = arctgu +1/v , если u = ![]() , v =
cosx.
, v =
cosx.
1.Найти объем тела, ограниченного поверхностями:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2.Найти массу пластинки, ограниченной линиями:
![]() ,
, ![]() ,
, ![]() ,
плотность
,
плотность ![]() .
.
3.Вычислить массу тела, ограниченного поверхностями:
![]() ,
, ![]() , плотность
, плотность ![]() .
.
4.Найти площадь поверхности ![]() ,
заключенной внутри цилиндра
,
заключенной внутри цилиндра ![]() .
.
5.Вычислить объем, ограниченный поверхностями:
![]() ,
, ![]() ,
, ![]() .
.
6.В интеграле по области D ![]() , D:{
, D:{ ![]() ,
, ![]() ,
, ![]() ,
, ![]() } перейти к новым переменным
} перейти к новым переменным ![]() ,
, ![]() .
.
1.
При каком значении параметра p
сходится знакочередующийся ряд 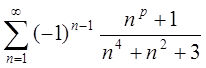 .
.
2.
Исследовать на сходимость ряд 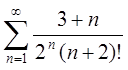 .
.
3.
Найти интервал сходимости
степенного ряда 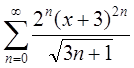 .
.
4.
Разложить в ряд Тейлора при x0 =2 функцию 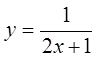 , найти
радиус сходимости.
, найти
радиус сходимости.
5.
Используя разложение в ряд функции
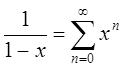 , найти сумму ряда
, найти сумму ряда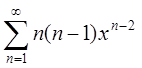 .
.
6.
Радиус сходимости степенного ряда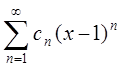 равен 2. Как ведет себя ряд в точке x=2:
равен 2. Как ведет себя ряд в точке x=2:
ряд сходится; ряд расходится; вывода о поведении ряда сделать нельзя , требуется дополнительное исследование. Дать пояснение.
7.
Указать номера расходящихся
рядов для которых необходимый признак сходимости не выполнен: 1) 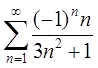 , 2)
, 2) 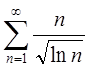 ,
3)
,
3) 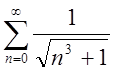 , 4)
, 4) 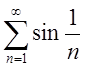 , 5)
, 5)
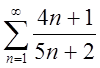 .
.
1. Определить тип дифференциальных уравнений первого порядка , найти общее решение:
§ xy' +2 y = cos x ;
§
x dy - y dx = ![]() dx;
dx;
§ y' cos x+ y sin x = 1.
2. Найти общее решение и частное решение, удовлетворяющее начальным данным,
для дифференциального уравнения:
y'' +4 y + 4 y = x2e 3 x ; y' (0) = 8, y (0)= 1.
3. Найти общее решение для дифференциального уравнения:
y y'' + y2 = 0.
3. Найти общее решение системы дифференциальных уравнений:
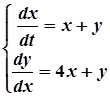
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.