Элементы зонной теории твердого тела, страница 7

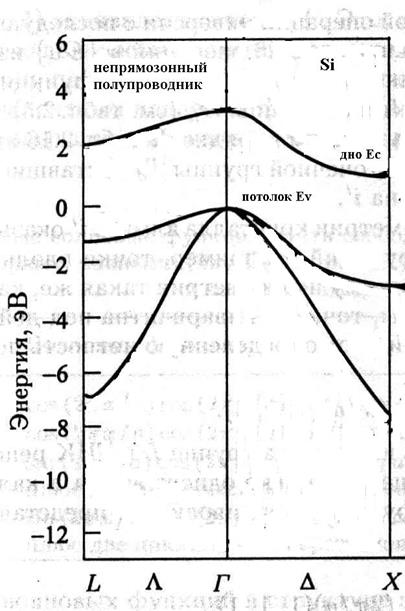
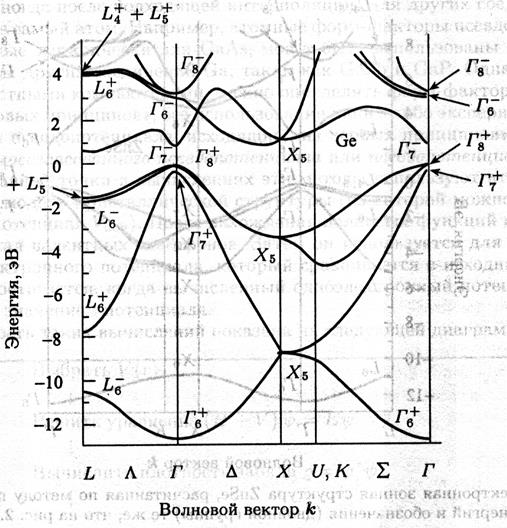
Рис. 3.6. Упрощённая зонная структура Si (слева) и зонная структура Ge (справа), данные из книги 2.1.

На рисунках 3.4 и 3.6 приведена структура энергетических зон для арсенида галлия, кремния и германия. Потолок валентной зоны, и дно зоны проводимости в GaAs (рис. 3.4) находятся в точке G (прямозонный материал), ширина запрещённой зоны составляет 1.43 эВ (при комнатной температуре). Эффективная масса для электронов изотропна и составляет 0.067 (и здесь и далее мы будем соотносить эффективную массу к массе свободного электрона). Валентная зона содержит: 1) зону тяжёлых дырок; 2) зону легких дырок; 3) отщеплённую за счет спин-орбитального взаимодействия зоны. Каждая из трёх зон двукратно вырождена по спину. Масса тяжёлых дырок составляет 1.12, масса лёгких дырок 0.5. Дисперсия дырок в GaAs непараболична (см. рис. 3.5). Кстати «близкий родственник» арсенида галлия и его постоянный партнёр по гетероструктурам – AlAs является непрямозонным полупроводником.

Кремний и германий являются непрямозонными материалами (рис.3.6). В кремнии дно зоны проводимости находится на направлении D зоны Бриллюэна (не на границе зоны). Таким образом, электроны в кремнии заселяют 6 X долин. Ширина запрещённой зоны кремния  - 1.1 эВ при комнатной температуре. Эффективная масса электронов X-долины в кремнии анизотропна, изоэнергетическая поверхность – эллипсоид вращения, вытянутый вдоль главных кристаллографических направлений. Продольная (тяжёлая) масса составляет 0.97, две поперечных массы равны 0.19. Массы тяжёлых и легких дырок составляют 0.5 и 0.16 соответственно.

В германии дно зоны проводимости находится на направлении L зоны Бриллюэна, на границе зоны в точке L. Таким образом, электроны в германии заселяют 8 половинок L долин (всего 4 L долины). Ширина запрещённой зоны германия  - 0.66 эВ при комнатной температуре. Эффективная масса электронов L-долины в германии также анизотропна, изоэнергетическая поверхность также эллипсоид вращения, вытянутый вдоль семейства эквивалентных <111> кристаллографических направлений. Продольная масса составляет 1.58, две поперечных массы равны 0.082. Массы тяжёлых и легких дырок составляют 0.3 и 0.04 соответственно. Изоэнергетические поверхности для электронов в кремнии и германии показаны на рисунке 3.7.

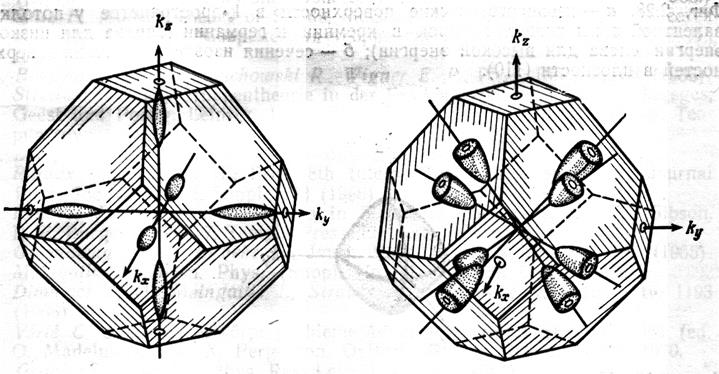
Рис. 3.7. Изоэнергетические поверхности долин электронов в кремнии (слева) и германии (справа).

Существуют оптические и электрофизические методики исследования энергетического спектра. Рассмотрим некоторые из них. Существование провала в энергетических уровнях (запрещённой зоны) приводит к возникновению оптической щели в поглощении света. Фотоны с энергией меньше чем ширина запрещённой зоны не могут возбудить электрон из валентной зоны в зону проводимости и не поглощаются кристаллом, то есть существует край поглощения. По положению края поглощения можно судить о ширине запрещённой зоны. При испускании света в процессе релаксации электрона с возбуждённого состояния вблизи дна зоны проводимости в валентную зону, энергия излучаемого фотона также соответствует ширине запрещённой зоны. То есть, используя данные фотолюминесценции, можно судить о ширине E_g. Тут главное различать переходы зона проводимости - валентная зона (так называемые фундаментальные переходы) от оптических переходов, связанными с примесями (дающими состояния в запрещённой зоне). Исследуя распределения по энергии (энергетический спектр) электронов, испускаемых кристаллом при освещении потоком фотонов (внешний фотоэффект), можно исследовать плотность состояний в валентной зоне. Тензор эффективной массы можно исследовать по резонансному поглощению по СВЧ-излучения в кристаллах в сильном магнитном поле. Резонанс имеет место, когда частота СВЧ-излучения совпадает с циклотронной частотой (циклотронный резонанс [1.7]). Этот эффект имеет как классическое, так и квантово-механическое объяснение. Циклотронная частота зависит от соотношения заряда к массе, и, в случае анизотропии эффективной массы, будет зависеть от направления магнитного поля.

Более подробно о методиках исследования зонной структуры можно прочитать в книгах 2.1-2.6.

Задание.

1) Нарисовать сечение изоэнергетической поверхности плоскостью (001) для электронов в кремнии. Показать направление продольной и поперечной массы.

2) Найти, при каком магнитном поле энергия циклотронного резонанса  для электронов в GaAs будет равна kT (T=300K).